Методи за решаване на системи уравнения

Какви са методите за решаване на системи уравнения?

В този раздел, ние обсъждаме три метода за решаване на системи уравнения. по-надежден от графичния метод, който се разглежда в предишния раздел.

метода на заместването

Този метод ще се използва в 7-ми клас за решаване на системи линейни уравнения. Алгоритъмът, който е разработен в 7-ми клас, е доста подходящ за решаване на системи уравнения на всеки две (не е задължително линейни) с две променливи х и у (разбира се, променливи могат да бъдат определени и останалите букви, няма значение). В действителност, този алгоритъм сме използвали в предходната алинея, когато проблемът с номера на двуцифрено доведе до математически модел, който е система от уравнения. Тази система от уравнения по-горе, ние решихме метод заместване (вж. Пример 1 в § 4).

Алгоритъм се използва техниката на заместване за решаване на система от две уравнения в две променливи х и у.

1. За да се изразят по отношение на х на система от уравнения.
2. Заместването експресията на у в другата уравнението на системата.
3. За решаване на уравнението за резултат х.
4. заместител алтернативно всеки от корените открити по уравнението на третия етап на мястото на X в експресионния ш от х, получен в първия етап.
отговор 5. Запишете под формата на стойност двойки (х, у), които са открити съответно на третия и четвъртия етап.

х променливите и Y, разбира се, равни права, така че със същия успех можем да в първата стъпка на алгоритъма не изразяват по отношение на х и х с у един уравнение. Обикновено избират уравнението, че е по-лесно, и изрази променливата от него, за които процедурата е по-ясно.

Пример 1 За решаването на системата от уравнения

1) изрази х по отношение на Y от първото уравнение: х = 5 - 3Y.
2) Заместването този израз за X в второто уравнение: (5 - 3 а) у - 2.
3) Ние решаване получената уравнение.

4) Заместването алтернативно всеки от получените стойности на Y във формулата X = 5 - ZU. Ако символът
5) двойка (2 1) и разтвори, посочени система от уравнения.

алгебрични метод допълнение

Този метод, подобно на метода на заместването, можете да излезете на курс Алгебра 7-ми клас, където тя се използва за решаване на системи линейни уравнения. Методът ние си спомняме следния пример.

Пример 2. За решаването на системата от уравнения

Умножете всички членове на първото уравнение с три, а второто уравнение е останало непроменено:
Ние се изважда второто уравнение от първи го уравнение:

В резултат на алгебрични добавянето на първоначалната система от две уравнения за получаване на уравнение лесно, отколкото първата и втората предварително определена система уравнение. Това просто уравнение ние имаме право да замени всяко уравнение на дадената система, като втората. След това се има предвид системата уравнения се заменя с по-проста система:

Тази система може да бъде решен чрез заместване. От второто уравнение заместваме този израз за база през първото уравнение, получаваме

Остава да заместим намерени х стойностите във формулата

По този начин, ние сме открити две решения:

Методът за въвеждане на нови променливи

С метода на въвеждане на нова променлива в решаването на рационални уравнения с една променлива, да се запознаем в хода на алгебра 8 клас. Същността на този метод за решаване на системи уравнения е един и същ, но от техническа гледна точка, има някои функции, които ние ще обсъдим в следните примери.

Пример 3 За решаването на системата от уравнения

Решение. Въвеждаме нова променлива След първото уравнение може да бъде пренаписана в по-проста форма: Нека да решим това уравнение за променливата Т:

И двете стойности отговарят на условието. и тъй като корените са рационални уравнения с променлива т. Но след това, когато всички, ние откриваме, че х = 2y, или
По този начин, на метода на въвеждане на нова променлива, ние сме били в състояние, така да се каже, "се разслояват" първото уравнение на системата е доста сложно на външен вид, две повече от простото уравнение:

Каква е следващата стъпка? И тогава всеки от двата прости уравнения, получени от своя страна трябва да се помисли системата на уравнението х 2 - у 2 = 3, което все още не сме се припомни. С други думи, проблемът се свежда до решаване на две едновременни уравнения.

Ние трябва да се намери решение на първата система, втората система, както и всички получени чифт стойности да се включат в отговора. Нека да решим първия набор от уравнения:

Ние използваме метода на смяна, най-вече защото тук всичко е готово за него: 2y замени изразът за х в второто уравнение на системата. получаваме

Тъй като х = 2y, ние откриваме, съответно x1 = 2, Х2 = 2. По този начин получава две решения дадена система (2, 1) и (-2, -1). Ние решаваме втория набор от уравнения:

Отново, ние използваме метода на смяна. 2 заменен експресията на база през второто уравнение на системата. получаваме

Това уравнение все още няма корени, следователно, системата от уравнения няма решение. По този начин, следва да се отговори, за да се включват само първите системни решения.

Методът за въвеждане на нови променливи за решаване на система от две уравнения с две променливи, използвани в две изпълнения. Първият вариант е нова променлива се въвежда и използва само в една система от уравнения. Такъв е случаят например в 3.Vtoroy опцията: две нови променливи са въведени и се използват едновременно и в двете уравнения на системата. Така че ще се случи в Пример 4.

Пример 4 За решаването на системата от уравнения

Въвеждаме две нови променливи:

Имайте предвид, че докато

Това ще позволи да се пренапише дадена система в много по-проста форма, но по отношение на новите променливи А и Б:

Ние прилагаме алгебричната добавяне на метод за решаване на системата:

Тъй като а = 1, тогава уравнение + 6 = 2 намираме: 1 + 2 = 6; 6 = 1. По този начин, променливи А и В, ние имаме едно-единствено решение:

Връщайки се към променливите х и у, получаваме системата от уравнения

Ние прилагаме алгебричната добавяне на метод за решаване на системата:

От уравнението от 2х + у = 3 намираме:
По този начин, променливите х и у, имаме едно решение:

отговори на:
В края на настоящия раздел с кратко, но достатъчно сериозна теоретична разговор. Вие вече сте известен опит в справянето с различни уравнения: линейни, квадратни, рационално, ирационално. Вие знаете, че основната идея на решението на уравнението е постепенното преминаване от едно уравнение с други, по-просто, но е еквивалентно на снимачната площадка. В предишния раздел ние въведохме концепцията за еквивалентност на уравнения с две променливи. Използвайте тази концепция и за системи от уравнения.

Две системи от уравнения с променливи х и у са призовани да бъдат равностойни, ако те имат един и същ разтвор, или ако двете системи не са решения.

И трите метода (заместване, алгебрични събиране и въвеждане на нови променливи), които сме описани в този раздел, е абсолютно правилни от гледна точка на еквивалентност на. С други думи, използването на тези техники, ние се замени една система от уравнения на друга, по-прости, но еквивалентна на изходната система.

Графичен метод за решаване на системи уравнения

Имаме сте научили за решаване на система от уравнения такива общи и надеждни методи, като например метода на заместването, алгебричната добавянето и въвеждане на нови променливи. А сега нека да си спомним с вас техника, която вече сте научили в предишния урок. Това е, нека да повторя това, което знаете за графичен метод на решение.

Метод за решаване на системата за уравнение е графично заговор за всеки един от конкретните уравнения са включени в тази система и са в една и съща координатната равнина, както и когато това е необходимо, за да намерите точки на пресичане на тези криви. За решаването на тази система от уравнения са координатите на точка (х; у).

Следва да се припомни, че системата от уравнения за графиките са склонни да имат нито един единствен правилен решение, или безкрайно много решения или не разполагате с решение на всички.

Сега, всеки един от тези решения в по-големи подробности. И така, системата от уравнения може да бъде единственото решение, ако преки, които са графики на уравнения се пресичат. Ако тези линии са успоредни, а след това на системата от уравнения има абсолютно никакви решения. В случай на съвпадение на системата директно фрези от уравнения, а след това такава система дава възможност да се намери набор от решения.

Сега, нека погледнем един алгоритъм за решаване на система от две уравнения с 2 неизвестни графичен метод:

• Първо, ние първо трябва изготвите график на първо уравнение;
• Втората стъпка е да се построят график, който принадлежи към второто уравнение;
• На трето място, ние трябва да намерим точката на пресичане на графиките.
• И в крайна сметка ние се координатите на всяка точка на пресичане, която ще бъде решаването на уравнения.

Нека разгледаме този метод по-подробно в примера. Дадено ни система от уравнения, за да бъде решен:

1. Първо, ние ще се изгради графика на уравнението: х2 + у2 = 9.

Но трябва да се отбележи, че в съответствие с графика на уравненията ще бъдат на кръг с център в основата, както и неговия радиус е равен на три.

2. Следващата стъпка е нанасяне това уравнение като: у = х - 3.

В този случай, трябва да се изгради линия и да намерят точката (0, -3) и (3, 0).

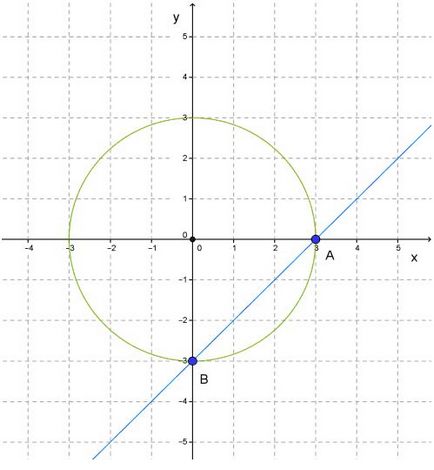
3. Да видим какво имаме. Виждаме, че линията пресича окръжността в две точки А и В.

Сега ние търсим координатите на тези точки. Виждаме, че координатите (3, 0) съответстват на точка А и координатите (0, -3), съответно, точка Б.

И това, което получаваме в резултат?

Получената пресичане на линията с кръга на (3, 0) и (0, -3) са само две решения на уравнения. От това следва, че броят на данни също е решение на тази система от уравнения.

Това означава, че отговорът на това решение са: (3, 0) и (0, -3).