Квадратна функция 2

Парабола състои от две части: една съхраняват в помещения I където положителни стойности на X и Y, а втората част - II в помещения, където отрицателни стойности X и Y са положителни стойности.

Ако отидете за един клон на параболата от -∞ до 0, ние отбелязваме, че функцията намалява един движи по друг клон на хиперболата от 0 до + ∞, а след това ние виждаме, че функцията се увеличава.

Ако уравнението на старши koeffitsienta на квадратна функция = 1, тогава графиката на квадратна функция има точно същата форма като у (х) = х 2 за всички стойности на други коефициенти.

Той има формата и се основава на "основни точки":

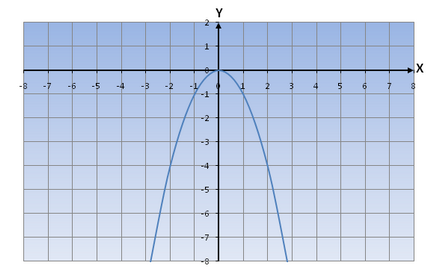
Парабола състои от две части: една съхраняват в помещения III, където отрицателни стойности х и у, и втора част - една четвърт и В, където положителни стойности на х и у стойности са отрицателни.

у (х) <0, при x ∈ (-∞;0) ∪ (0;+∞)

Ако отидете за един клон на параболата от -∞ до 0, ние отбелязваме, че се увеличава функционира като един движи по друг клон на хиперболата от 0 до + ∞, тогава ние виждаме, че функцията намалява.

1) домен на функцията:

2) Област на стойности на:

3) Най-голямата и най-малката стойност на функцията:

Ако<0, то Yнаиб =0,Yнаим нет.

Ако> 0, toYnaim = 0, Ynaib не.

4) Y (х) = х 2 - дори функция (t.k.f (-x) = х 2 = (- х) 2 = е (х)).

Графиката е симетрична спрямо оста OY.

5) ограничени функции:

Ако> 0, е ограничена по-долу.

Ако<0 , функция ограничена сверху.

6) Функция пресича вол OY ос и точката (0, 0)

Преместването parabolyy (х) = х 2

Ако добавим и постоянното г (D, където всяко число), като summand да X. движение ще се случи по оста на параболата (заедно с вертикална асимптота).

В този случай, уравнението на функцията ще бъде:

Ако D> 0 (у (х) = (х + г) 2). графиката на функцията се движи по вол ос наляво.

Например, да разгледаме уравнението у = (х + 2) 2

Ако г<0 (y(x)=(x-d) 2 ). то график функции передвигается по оси oX вправо.

Например, да разгледаме уравнението у = (х-2) 2

Ако добавим и постоянна в (в които всяко число) на X 2 като събираемо, няма да има движение на парабола ос Oy (с хоризонтална асимптота)

В този случай, уравнението на функцията ще бъде:

Ако в> 0 (у (х) = (х) 2 + в), след това графиката на функцията на OY движи аксиално нагоре.

Например да разгледаме уравнението у = (X) 2 2

Ако в <0 ( y(x)=(x) 2 -c ), то график функции передвигается по оси oY вниз.

Например да разгледаме уравнението у = (X) 2 -3

И намери корените на дискриминантата

1) 1) Ако D> 0, тогава уравнението ос 2 + BX + С = 0 има две решения, уравнението у = ос 2 + BX + в 2 има точка на пресичане с оста ОХ:

Ако> 0, функцията за графика ще има приблизителна форма:

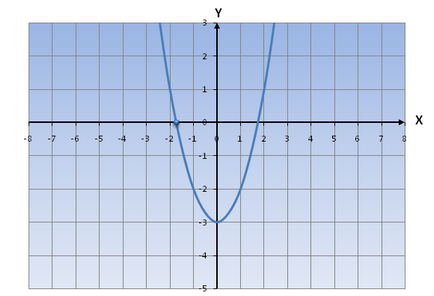
2) Ако D = 0, тогава уравнение ос 2 + BX + С = 0 има разтвор на 1 => uravneniey = брадва 2 + BX + в 1 е точката на пресичане с оста ОХ.

Ако> 0, функцията за графика ще има приблизителна форма:

3) Ако D<0, то уравнение ax 2 +bx+c=0 не имеет решения, => uravneniey = брадва 2 + BX + в още няма общи точки на пресичане с оста ОХ.

Ако> 0, функцията за графика ще има приблизителна форма:

Координати на върха на параболата

Има координати на върха на параболата чрез тези формули:

Линия, преминаваща през върха на параболата е оста на симетрия на параболата.

В точката на пресичане с osyuoY

Тъй като абсциса всяка точка лежи на оста OY нула да се намери точката на пресичане на парабола Y = брадва 2 + BX + в с ос OY, необходими в уравнението на параболата вместо Xpodstavit 0, тогава Y (0) = C.

Алгоритъм за построяване на квадратното парабола

1) посока клонове.

2) координатите на върха на параболата.

3) Корените на дискриминантата.

4) Допълнителна точка.

5) Изграждане на графиката.

Построява функция у = х 2 -6x + 15

В квадратичен трином х 2 -6x + 15, за да се изрази квадрат разликата използване формула Инициали размножаването на.

Основната формула: (а ± б) = х 2 2 ± 2ab + б 2.

Ние експресира квадрат разликата: х 2 -6x + 15 = (х 2 -6x + 9) 6

Поставянето на формулата: (х 2 -6x + 9) + 6 = (х-3) 2 6

Получават функция у = (х-3) 2 6

Отбелязваме, че графиката на функцията е изместен от 3 до ОХ ос надясно и 6 OY аксиално нагоре.

Следователно, графиката на функция Y = (х-3) 2 6 ще изглежда така:

Построява функция у = х 2 + 8x + 17

В квадратичен трином х 2 + 8x + 17 за изразяване на квадрат разликата използване формула Инициали размножаването на.

Основната формула: (а ± б) = х 2 2 ± 2ab + б 2.

Ние експресира квадрат разликата: х 2 + 8x + 17 = (х 2 + 8x + 16) 1

Поставянето на формулата: (х 2 + 8x + 16) + 1 = (х + 4) 1 2,

Получават функция у = (х + 4) 2 + 1,

Отбелязваме, че графиката на изместен наляво от 4 вол и 1 OY аксиално нагоре.

Следователно, графиката на функция у = (х + 4) 1 2 ще изглежда така:

За да разширите квадратен тричлен, използвайки този алгоритъм:

1) експресира квадрат разлика от това трином, използвайки формули Инициали умножение;

2) Въвеждане, получената формула;

3) "чете" графиката на отместване спрямо осите на координати;

4) изграждане на графика.