Видове Матрицата Матрици

ЕДИНИЦИ 1 Елементи на линейната алгебра

Матрицата, видове матрици. Операции на матрици. матрични елементи. Обратното матрица

Определение: Матрицата се нарича правоъгълен масив от числа, състоящи се от м редове с еднаква дължина, или п колони еднаква дължина.

Aij - матрица елемент, който е в I-ти ред и к-тата колона.

Основните видове матрица:

¾ квадрат (матрица с равен брой колони и редове);

¾ транспонират (може да се получи чрез промяна на редовете и колоните на матрицата в места матрица размер за тази трансформация ще бъде измерение на матрицата А Т.);

Три четвърти блок (квадратна матрица, елементите на основната диагонала на които са равни на един, а другите са нула)

Матрици са широко използвани в математиката за система компактен запис от линейни алгебрични или диференциални уравнения. В този случай, броят на редовете на матрицата съответства на броя на уравнения и броя на колоните - броя на неизвестни. В резултат на решаване на системи линейни уравнения се редуцира до операции на матрици.

следните алгебрични операции са дефинирани за матрицата:

¾ присъединителни матрици с еднакъв размер;

¾ матрица умножение с подходящ размер (матрица като колони могат да се размножават в дясно от матрица като редове);

¾ включително умножаване с вектор матрица (от обичайната принципите на матрица умножение на вектор в този смисъл, че частен случай на матрицата).

Помислете за експлоатация на матрици по-подробно.

1. Добавянето на матрици А + В е матрица С за намиране на работа, всички чиито елементи са двойки сума на всички съответни елементи на матрици А и В, т.е., всеки елемент на матрицата С равна на

2. увеличи броя на матрицата # 955; (Символ: # 955 А) е за конструиране на матрицата В, чиито елементи са получени чрез умножаване на всеки елемент на матрицата на тази фигура, т.е. всеки елемент от матрица В е равно на

3. умножение на матрици (символ: АВ, с по-малко умножение знак) - е операция за изчисляване на матрица C чиито елементи са равни на сумата от продуктите на елементи в съответния ред на първия мултипликатор и втората колона (ред умножение колона).

Броят на колоните на матрицата трябва да съответства на броя на редовете в масив В. Ако матрицата има измерение. матрица B -. След това размерът на продукта AB = С е. Виж Фигура 1.

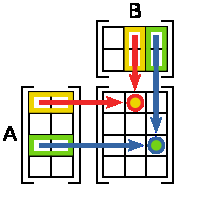
Фигура 1 - Правилото на умножение на две матрици

Пример 1: Виж A + 2В, ако. ,

Пример 2: Виж. ако.

Пример 3: За решаване на уравнението на матрица :,

.

Определение: детерминанта на матрица А е означен като: Det (А), | А | или # 916; A.

Формулата за изчисляване на детерминанта на втория ред:

Формули за изчисляване на детерминантата на третия ред:

а) разширяване на елементите на първия ред:

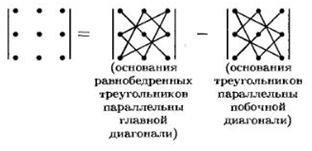
б) по правило звездичка (или Sarryusa)

Основните свойства на детерминанти.

Собственост 1. детерминанта не се променя от транспониране, т.е.

Забележка. Следните свойства на детерминантите ще бъдат формулирани само за низове. Когато този имот 1 означава, че същите качества ще притежават и колони.

Имоти 2. Когато се умножи елементи на детерминанта линия за редица детерминантата се умножава с този номер, т.е.

Имоти 3. определящ фактор, който има нула низ е 0.

Имоти 4. детерминанта като две равни редове 0.

Собственост 5. определящи две линии, които са пропорционални на нула.

Имоти 6. Когато се движи двата реда детерминантата се умножава по -1.

7. Стойността на собственост на детерминанта не се променя, ако елементите на един ред, за да добавите съответните елементи на друг ред, умножени по един и същ номер.

8. Определяне на Мала съответстващ на този елемент Aij на детерминанта на третия ред, наречен втори ред детерминанта, получени с анулиране на този ред и колона по чието пресичане е активен елемент, т.е. I-ия ред и к-тата колона. Непълнолетни Aij, съответстващи на този елемент ще бъде означен с MIJ.

Пример 4: незначително M12. а12 съответния елемент. ще бъде определящ фактор. който е получен с анулиране на детерминанта на първия ред и втората колона.

Определение. Кофактор на определящ елемент Aij се нарича непълнолетен MIJ. умножена по (1) I + J. Кофактор Aij означава елемент Aij.

От дефиницията виждаме, че алгебрични връзката между елемент и комплемент се изразява чрез незначително Aij = (-1) I + J MIJ.

Пример 5: Dan детерминанта. Намери A13. A21. A32.

Определение. Ако А - квадратна матрица, инверсната матрица е това матрица, означен с А -1 и отговаря на състоянието. (Това определение се въвежда, по аналогия с номера на умножение). се въвежда Концепцията на обратна матрица само за квадратни матрици.

Теорема. За да квадратна матрица А има обратното, е необходимо и достатъчно му детерминанта да е различен от нула.

Така че, да се намери е необходимо обратното на матрица:

1. Намерете детерминанта на матрица A.

2. Намерете матрица транспозиция на получената матрица.

3. Намери кофактори Aij на матричните елементи А и Т композиране на матрица, чиито елементи са цифрите Aij.

4. Умножете матрица, получена в етап 3

Пример 6: Виж обратната матрица А -1. ако и валидиране.

. . За да проверите използва формулата. къде.