Урок - задължително и косинус на сумата от аргументите
Кратко описание на документа:
В хода на изследването на студентите тригонометрия са били изложени на функциите на основните им свойства, поведението на героя. Сред тези основни функции са периодични функции на синус, косинус, тангенс и котангенс. Те имат различни периоди и спецификации.
Учениците научиха да изградят свои графики и функции за анализ на данни. Изследвани домейн стойности домейни, увеличаване и намаляване пропуски и т. П.
Един от основния основен формула е сумата на синус и косинус на сумата, която често се използва при решаване на различни проблеми. Когато домашна работа, или на различни независими и контролни работи студенти несъмнено ще бъдат изправени пред необходимостта да се използват данните на формулата. Ето защо е важно да се разбере правилно този урок, за по-добро и по-дълго се помни.
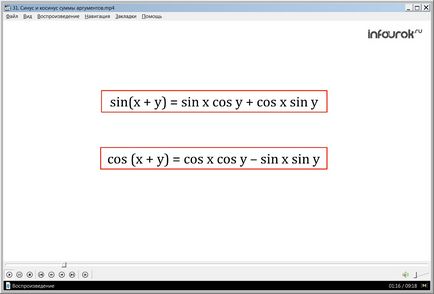
тези формули са оградени в червено поле, като по този начин се набляга на важността на паметта ще бъде демонстриран в първата част на презентацията. Виждаме, че те се различават един от друг. Не забравяйте формулата няма да е трудно, ако се прилага правилно в практиката.
Говорителят обясни на учениците как искате да прочетете тези формули правилно. Някои учители изискват учениците да играят в словесна форма на тези формули с цел разработване на математически език. Така че, трябва внимателно да слушат говорещия и да го запишете, ако е необходимо в тетрадка.
След е първият практически пример. Вие искате да намерите синуса на 105 градуса. Говорител предлага решения за този пример резултат под ъгъл от 105 градуса, като сумата на два ъгъла, а именно 45 и 60, Sines и уюта, които знаят учениците и могат да си спомнят като адресирано до таблицата със стойностите на тригонометрични функции.
Тези таблици са за да се показват с цел напомняне. Продукция на стойностите, които имаме нужда. Освен напомни формула количество задължително аргумент, който се използва за решаване на друг пример. В последния етап специфични стойности са заместени в таблицата, и се получава отговор.
Вторият пример предлага да се опрости комплекс експресия, съдържащ тригонометрични функции. За решаване на проблема с помощта на двете формули обсъдени по-рано. Разтворът се демонстрира стъпка по стъпка. Това на учениците да разберат къде са ценностите показват таблица с тригонометрични ценности и акцентира върху клетките, използвани.
В резултат на това, както в предишния пример, се показва отговора.
Третият пример е подобен на първия, четвъртия, и освен това решението е по-сложно и интересно. Трябва да се намери косинуса на сумата от аргумента, ако знаете някои от данните. За предпочитане разгледа проблема с учителя или преподавател. Ако студентът е умен и добър математическа рамка, той ще бъде в състояние да разберат и независимо дали пропуснатата урок или искате да ги възстановите в паметта. За да укрепи разбирането на тези примери, ние можем да предложим на студентите от няколко други подобни примери от училище учебника, решаването на които те ще трябва да се използва формулата на синус и косинус сума от аргументите.
Една пета пример за сложността е на първо място. В него се предлага да се реши тригонометрични уравнения, които трябва да бъдат добре да се помни и да разберете как вие използвате тригонометрични формули.
Решението е много ясен и подробен начин. Говорителят обяснява всяка стъпка, не пропускайте всеки важен момент. От дясната страна на разтворите, съдържащи се мехурчета и формули, които се прилагат при извършване на работата.
Ние вече са запознати с тригонометрични функции, техните графики, научили за решаване на тригонометрични уравнения. И сега се пристъпи към изучаване на тригонометрични формули, чрез които можем да трансформират тригонометрични изрази.
Най-важните са формула тригонометрия, обикновено се нарича сумата от синус и косинус на сумата.
грях (х + у) = грях х защото у + защото х грях у,
COS (х + у) = COS х COS у - SIN у х грях.
Тези уравнения могат да се четат като сбор от две синусови ъгли е равен на сбора на продукта между синуса и косинуса на ъгъла на първия ъгъл, а вторият продукт на косинус и синус на първия ъгъл на втория ъгъл;
косинус на сумата от два ъгъла е равен на разликата между продукта на косинус на тези ъгли и продуктът на сбора на тези ъгли.
От тези формули можем да извлечем почти всички формули на тригонометрията.
Как да използваме същата формула сумата от синус и косинус на сумата. Помислете за дадените примери, че всяка формула може да се прилага като "ляво" и "дясно".
Пример 1. Изчислява грях 105 °.
Решение. Представлява сто и пет градуса като сума от 105 ° = 45 ° + 60 °. Ние знаем, че грехът 45 ° = 45 °, защото =. грях 60 ° =. COS 60 ° =.
Покажи маса на ценности
Заместването на тези стойности във формулата за сумата от задължително
грях (х + у) = грях х защото у + защото х грях у,
Togdasin 105 ° = грях (45 ° + 60 °) = грях 45 ° COS 60 ° + 45 ° COS грях 60 ° = + ∙ ∙ = =.
(Сто и пет градуса задължително е синуса на сумата на четиридесет и пет градуса и шестдесет градуса и е равна на тази сума фракция, числителя на който е корен на сбора от двете, и основата на шест, и знаменателят -. Четири)
Отговор: грях 105 ° =.
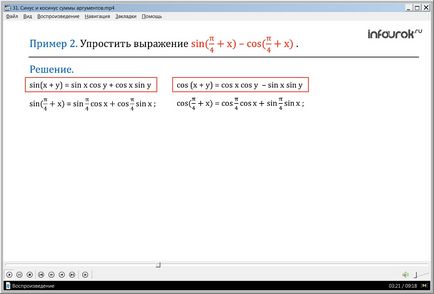
Пример 2. За да се опрости експресия греха (+ х) - COS (+ х) (разлика задължително пи разделен на четири, плюс X, и косинус на пи разделен на четири, плюс X).
Решение. Нанесете задължително формула за намалено количество греха (+ х)
грях (х + у) = грях х защото у + защото х грях у,
След намаляване на грях (+ х) = грях + защото палка Sinh.
Прилагане на формулата на сумата от COS на косинус Умалител (+ х)
COS (х + у) = COS х COS у - SIN у х грях.
Умалител COS (+ х) = защото + грях палка Sinh
грях (+ X) - COS (+ х) = грях защото х + х защото грях - защото защото + грях грях х х
Покажи маса на ценности
От стойностите на таблица се намери стойността на греха и защото
грях = Кос =, заместване на тези стойности в израза и да получат:
= ∙ + ∙ палка Sinh - ∙ + ∙ палка Sinh
Палка ∙ - ∙ = 0 палка, Sinh е ∙ ∙ + Sinh, че е 2 ∙ ∙ Sinh Sinh получите.
грях (+ X) - COS (+ х) = грях защото х + х защото грях - защото защото + грях грях х = х
= ∙ COS х + ∙ грях х - ∙ защото х + ∙ грях х = 2 ∙ ∙ грях х = грях х. Това е пълна числено решаване.
Отговорът е грях (+ х) - COS (+ х) = Sinh.
Пример 3. Изчисли грях 17 ° COS 13 ° + cos17 ° грях 13 °. (Sine седемнадесет градуса, умножени по косинус от тринадесетте степени плюс косинус на седемнадесет градуса, умножени по синуса на тринадесет градуса).
Решение. Този израз може да бъде "пъти" в сумата от аргументите задължително 17 ° и 13 ° (т.е.. Използвайте "отдясно наляво" задължително формула за сумата).
грях (х + у) = грях х защото у + защото х грях у,
грях защото 13 ° + защото грехът 13 ° = грях (+ 13 °) = грях 30 ° = (сума на продукта на синуса на седемнадесет градуса косинус на тринадесет градуса и работи косинус седемнадесет градуса задължително тринадесет градуса равни на синуса на сумата от седемнадесет и тринадесет градуса равна на синуса на тридесет степени, равни на една секунда).
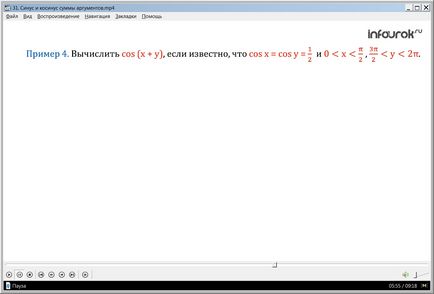
Пример 4. Изчислява COS (х + у), ако знаем, че COS х = у = COS
0 х (X е по-голямо от нула и по-малко от две PI) в 2p (у пи повече от три от две, но по-малко от две PI).
Решение. Ние използваме формулата на сумата на косинус:
COS (х + у) = COS х COS у - SIN у х грях.
Стойности cosx и уютна комплект. Изчисляваме ценности и sinx siny. Ние използваме основния тригонометрични идентичност: грях 2 т + защото 2 т = 1. Ние имаме: грях 2 х = 1 - защото 2 х. и като х = COS. тогава заменен с формула и получаване = 1 - () 2 = 1 - =.
грях 2 х = 1 - защото 2 х = 1 - = Това цифров пълно разтваряне.
От състоянието на аргумента X принадлежи към първото тримесечие, а в него синуса е положителна. Затова SINH =.
По същия начин, грях 2 у = 1 - защото 2 у = 1 - =. но аргумент у принадлежи към четвъртото тримесечие, и то задължително е отрицателен, така че у грях = -.
Заместването на стойностите, получени и дадени във формула за сумата на косинус получи COS (х + у) = ∙ - ∙ = + = 1.
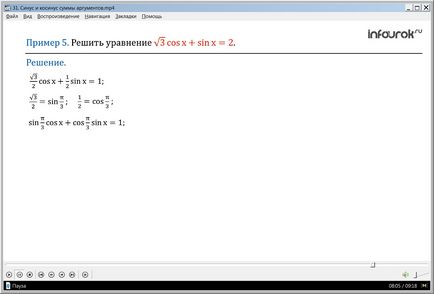
Пример 5 решаване на уравнение cosx + sinx = 2.
Разделете двете страни от две, ние получаваме cosx + sinx = 1
Ето уравнението на форма формула задължително сумата от два ъгъла:
и припомни, че = грях. а = COS.
Покажи маса на ценности
защото х + грях х = 1,
sincos х + защото грях х = 1,
После лявата страна на уравнението е дясната част на формулата за сумата от синусови и х аргументи. Така лявата част на експресията е равно на грях (+ х)
Ние се намери стойността на х