Уравнение с три неизвестни, математика
62. Един уравнение с три неизвестни. Да предположим, че имаме уравнение
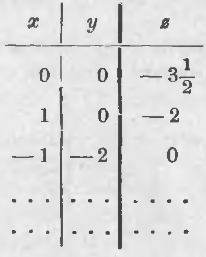
В това уравнение може да се разглежда като запис задачи: да се намери числени стойности за X, Y и Z, за да трином 3x + 4у - 2z е равен на броя 11. Така че това е уравнение с три неизвестни. Така че как можем да решим един уравнение с едно неизвестно, че на пръв поглед има идеята, че има две неизвестни, така да се каже излишно, и те могат да се дават произволни стойности. Всъщност, ако, например, да се редица Y 3 и Z номер 5, ние получаваме уравнението в един неизвестен:
Обърнете други номера за Y и Z. Например, нека
Тогава ние получаваме уравнението:
Продължаване на работата по стигаме до извода:
Едно уравнение с три неизвестни, има безкрайно много решения, и за тях е необходимо да се даде две неизвестни произволни стойности.
Резултатите от тази работа може да се запише в таблицата (ние с изключение на две вече открити разтвори, записани в него е друг, който се получава чрез въвеждане у = 1 и Z = -2):
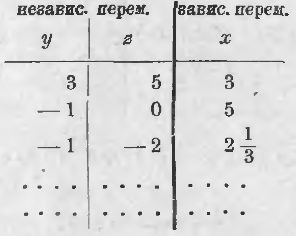
Тъй като Y и Z за вземем произволни стойности, те са независими променливи, и х е зависимо от (от) променлива. С други думи: X е функция от Y и Z.
За да се улесни получаването на разтвора на това уравнение, може да се определи от х до у, и Z. получаваме:
3x + 4Y - 2Z = 11; 3x = 11 - 4Y + 2Z;
х = (11 - 4Y + 2Z) / 3.
Ние даваме, например. стойности: у = 5 и г = 1; ние получаваме: х = (11-20 + 2) / 3 = -2 (1/3), и др ...
Нека да уравнението
Да приемем, х и у като независими променливи, и Z - зависимости и да се определят чрез Z х и у
-2z = 7 - 3x + 5Y; 2Z = 3x - 5Y - 7; Z = (3x - 5Y - 7) / 2
Сега е лесно да се направи таблица решение: