Триъгълник и кръг

Кръгът е описано около триъгълника се нарича. ако всички върховете на триъгълника са разположени на кръга.

Неговият център на еднакво разстояние от всички върхове, а след това трябва да има в точката на пресичане на перпендикулярни ъглополовяща на страните на триъгълника.

Следователно, за всеки триъгълник може да бъде описан като кръг, от средата на перпендикуляра към страните се пресичат в една точка.

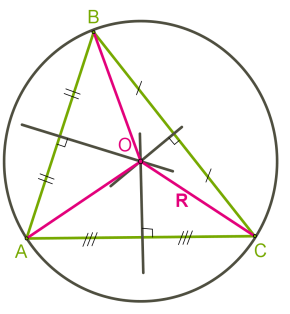
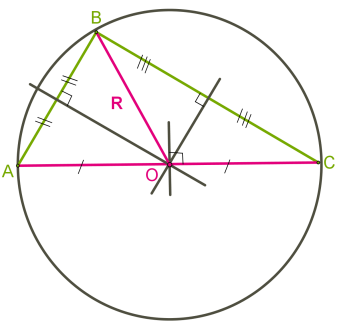
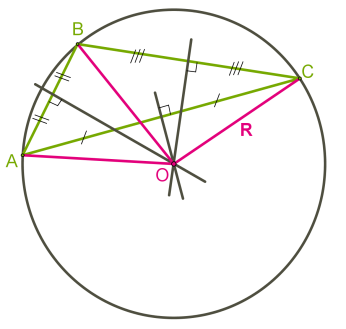
За малък правоъгълен триъгълник е в центъра на кръга, в триъгълника.

Друга ситуация, с правоъгълни и тъпи триъгълници.

Кръг, вписан в триъгълник

Кръг вписан в триъгълник се нарича. ако всички страни на триъгълника докосват кръга.

Неговият център на еднакво разстояние от всички страни, тоест, трябва да е в точката на пресичане на ъглополовящи на триъгълника.

Следователно, във всеки триъгълник кръг може да се впише, като ъглополовящата на триъгълника се пресичат в една точка.

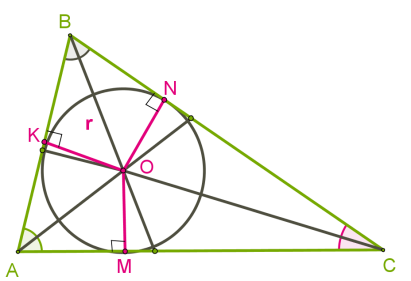
От ъглополовящата на ъгли на триъгълник винаги се пресичат във вътрешността на триъгълника, в центъра на всички триъгълници вписан кръг е в триъгълници.

В равностранен триъгълник съвпада разполовяване, медианите и височина, т.е., тези сегменти са също midperpendiculars. Това означава, че центровете на определена и вписан кръг на едни и същи.

Радиусът на описаните окръжности

R = 03 февруари часа. Следователно, R = 3 месец март.

Радиусът на вписаната

г = 1 март часа. където \ (з \) - височината на триъгълника.

Ако е дадена страна на триъгълника \ (а \), след H = 2 месец март.

Следователно, R = на 03 юни

Радиусът на описаните окръжности

R = 01 Февруари С. където \ (в \) - хипотенузата.

Радиусът на вписаната

R = S δ стр. където \ (р \) - semiperimeter.

Радиусът на описаните окръжности

R = на ⋅ б ⋅ в 4 ⋅ S δ

R = на α 2 грях. където α - ъгъл противоположната страна \ (а \).

ако S δ = ABC 4 R. тогава R = ABC 4 S δ; ако S δ = р ⋅ R. тогава R = S δ стр