Сумиране на определени последователности

следователно
1 2 + 2 2 + 3 2 +. + N 2 = (п + 3 п 2 + (1 + 2 + 3 +. + N)) / 3.

защото
1 + 2 + 3 +. + N = N (п + 1) / 2,
1 2 +2 2 + 3 2 +. + N 2 = (п + 3 п2 + п (п + 1) / 2) / 3 = п (п + 1) (2 п + 1) / 6.

Количеството на четвърти силите на първите N номера получи арабика математик Ал Karadzhi (X-XI см.). Той построен квадрат със страни (1 + 2 + 3 + + (п -. 1) + п). и в нея - друга квадрат (в близост до ъгъла на първата квадрат) със страна (1 + 2 + 3 + + (п -. 1)). Разликата от тези две полета е Gnomon чиято ширина п. голяма страна е равна на (1 + 2 + 3 + + (п -. 1) + п) = N (п + 1) / 2. Площта на Гномонът 2 N 2 (п + 1) / 2 - п 3 2 = N . Ако сега в квадрат със страна (1 + 2 + 3 + + (п -. 1)), за да определя същия ширина Гномонът (п - 1). площта му е (N - 1) 3. продължаващо по този начин, в крайна сметка стигна до площада на оригиналния 1. Площта на квадрат със страна (1 + 2 + 3 + + (н. - 1) + N). по този начин разделя на gnomons, части на които са равни на п 3. (М - 1) 3. 3 3. 2 3. и квадратния областта на 1 = 1, 3. Така, 1 3 + 2 3 + 3 3 +. N + 3 = (1 + 2 + 3 +. + N) 2 = (п (п + 1) / 2) 2.

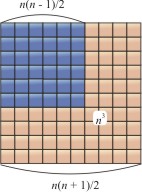
Фиг. 8. Гномонът на раната зона п 3

Интересна последователност смята френският философ схоластичен XIV век. - Н. Orem. Чудеше се какво ще бъде равна на средната скорост (в терминологията на средната "интензитета", по-общ термин, но сега ние сме достатъчно да се счита средната скорост) интервалът е 2, ако този период е разделен на части, отговарящи на намаляваща геометрична прогресия: 1, 1/2, (1/2) 2 (1/2) 3. и във всяка точка на процент се увеличава в аритметична прогресия 1, 2, 3, 4. за да се реши този проблем, е необходимо да се оцени експресията на тип: 1 # X2219; 1 + 2 # X2219; (1/2) + 3 # X2219; (1/2) 2 + 4 # X2219; (1/2) 2. сумата на броя на Orem представени като областта на стъпка като фигура, направена от един срещу друг на правоъгълници, всяка от които е с височина от 1, и ширината на дъното 2, покриваща един допълнителен 1/2. (1/2) 2 и т. Г. цялата фигура е разделена чрез вертикални линии на парчета с широчина 1, 1/2, (1/2) 2 и т. D.

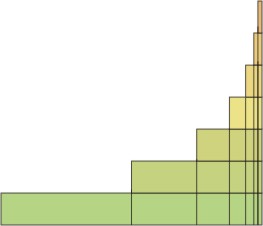
Фиг. 9. Няколко Orem

Тази цифра, всъщност, не друг, а скоростта на графиката на височина в най-лявата му страна е равна на 1, а след това 2, след това 3 и т.н. Сумата от редица равна на площта на цялата фигура, заедно с факта, че районът може да се намери по различен начин ..: площта на правоъгълника е равно на 2, по-висока 1, след това 1/2 (1/2) 2, и т.н. - .. не се занимават с нищо друго освен геометрична прогресия, количеството на които е равно на 4. Средната скорост на целия интервал равна на общата площ (4), разделена на дължината на празнината (2) - т.е. 2, скоростта на втория празнината. Плавно намаляване геометрична прогресия и броя разглежда от Orem, имат ограничен размер. И от друга серия? Ясно е, че за да може сумата от безкраен брой от гледна точка на серията ще бъде равен на една крайна величина, което трябва да направите определен брой членове ще са склонни към нула, тоест, като се започне с достатъчно голям брой, за да станете по-малко от който и да е предварително определена стойност. Но това не е достатъчно. Има, себе си, последователност тенденция към нула, така че сумата от серията се стреми към безкрайността. Orem първо да докаже, че хармоничните серии

не summable, че е сумата от неговите членове н като н увеличава рано или късно ще надхвърли всяка предварително определена стойност. Доказателството се основава на факта, че

1/3 + 1/4> 2/4 = 1/2,
1/5 + 1/6 + 1/7 + 1/8> 1/2,

8 и следните номера в размер на повече от 8/16 = 1/2, и така нататък. Г. А от редица 1 + 1/2 + 1/2 + 1/2 + и т. Г. Очевидно увеличава до безкрайност, и хармоничните серии, също отива до безкрайност. Този факт понякога се илюстрира по следния начин.

Тухлите са поставени един върху друг, така че те не попадат: за това центъра на тежестта на горните тухлите трябва да се намира в рамките на по-ниска база. Ако две тухли, може да се измести по отношение на другата половина на дължина. Ако три, след това средната спрямо дъното да бъде изместен с една четвърт, тъй като центъра на тежестта на първите две се намира по средата между центровете на масата на всеки. Ако четири, а след това по отношение на дъното на следващия тухлата да бъде изместен от една шеста от дължината на една тухла. И така нататък. D. Като цяло, изглежда, че, с неограничен брой идеални тухли, на върха може да бъде променен спрямо дъното независимо от разстоянието и като хармонична поредица може да се произволно голяма стойност.

В допълнение към безкрайни суми могат да се считат безкрайно продукти. Първият от тях, въведен от F. Wyeth. Предвид проблема с квадратура кръга, Wyeth подадена отношението между площта на правилен многоъгълник с п и 2 п страни вписан в същия кръг с радиус R. Всеки от тези полигони може да бъде разделена на 2 п триъгълници с връх в центъра на ъгъла на многоъгълник и връх, равна на 180 ° / п. при първата от тях, всеки такъв триъгълник е правоъгълен, а вторите равнобедрен. Тъй като те имат една обща височина, съотношението на техните територии е равна на съотношението на бази. На R COS първата основа (180 ° / о). втората съотношение зона R. полигони равен на съотношението на области на тези триъгълници т. е. COS (180 ° / о).

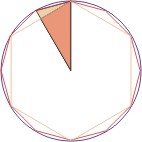
Фиг. 10. Степента на площ е съотношението на триъгълници бази