Sine, косинус, тангенс и котангенс в тригонометрията

В тази статия, ние показваме как да се предостави определения на синус, косинус, тангенс и котангенс на ъгъла, а броят на тригонометрията. Тук говорим за стъпваща на които даваме примери за записи, които дават нагледна илюстрация. В крайна сметка ние направим паралел между определенията на синус, косинус, тангенс и котангенс в геометрията и тригонометрията.

Навигация в страниците.

Определяне на синус, косинус, тангенс и котангенс

Един остър ъгъл в правоъгълен триъгълник

Разбира известен геометрия определяне синус, косинус, допирателна и котангенс малък ъгъл в правоъгълен триъгълник. Те са дадени като съотношение на страните на правоъгълен триъгълник. Това са техните отчети.

Синуса на малък ъгъл в правоъгълен триъгълник - е съотношението на другия крак на хипотенузата.

Котангенс на малък ъгъл в правоъгълен триъгълник - съотношението на съседна страна на обратното.

Има също така въведе нотация задължително, косинус, тангенс и котангенс - грях. защото. и TG CTG съответно.

Например, ако ABC - правоъгълен триъгълник с десния ъгъл С. задължително на остър ъгъл равен на съотношението на другия крак с хипотенуза BC AB. т.е. sin∠A = BC / AB.

Тези определения ще дадат възможност да се изчислят стойностите на синус, косинус, тангенс и котангенс малък ъгъл от познатите странични дължини правоъгълен триъгълник и като се знаят задължително, косинус, тангенс, котангенс, а дължината на една от страните да се намери дължината на другите страни. Например, ако знаем, че катет AC правоъгълен триъгълник и хипотенузата е равна на 3. 7. AB е равно бихме могли да се изчисли косинус на остър ъгъл А, по дефиниция: cos∠A = AC / AB = 3/7.

ъгъл на завъртане

В тригонометрията ъгъл да започне да изглежда по-широк аспект - въвеждане на концепцията за ъгъла на завъртане. Големината на ъгъла на завъртане, за разлика от малък ъгъл, не се ограничава до обхвата от 0 до 90 градуса, ъгълът на въртене в градуси (в радиани) може да се изрази във всякакво реално число от -∞ до + ∞.

В тази връзка, тъй като определянето на синус, косинус, допирателна и котангенс не е остър ъгъл, а ъгълът на всяка величина - ъгъл на въртене. Те са дадени от координатите х и у А1 точка. в който така наречената начална точка А (1, 0) след завъртане на ъгъл α около точка О - започващи правоъгълна Декартова координатна система и центъра на единица кръг.

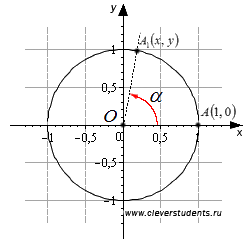
Синуса на ъгъла на завъртане α - е ординатата на точка А1. т.е. sinα = у.

Котангенс на ъгъла на завъртане α е съотношението на абсциса А1 точката си ордината, т.е. ctgα = X / Y на.

Синуса и косинуса се определят за всеки ъгъл α. защото винаги може да се определи абсцисата и ординатата на точката, която се получава чрез завъртане на началната точка при α ъгъл. А допирателна и котангенс не са определени за всеки ъгъл. Тангента не е определено за тези ъгли алфа. в които началната точка премества в точката с абсцисата на нула (0, 1) или (0, 1). и това става под ъгъл от 90 ° + 180 ° · к. k∈Z (π / 2 + π · к RAD). Всъщност, при тези ъгли на въртене експресия tgα = Y / х е безсмислено, тъй като има участък от нула. Що се отнася до котангенс, не се определя за такива ъгли алфа. в които началната точка се движи до точка с нулева ордината (1, 0) или (1, 0). както е в случая с ъгли от 180 ° · к. k∈Z (π · к RAD).

Така функциите синус и косинус са определени за всички ъгли на въртене, допирателна дефинирани за всички ъгли освен 90 ° + 180 ° · к. k∈Z (π / 2 + π · к Rad) и котангенс - за всички ъгли освен 180 ° · к. k∈Z (π · к RAD).

Определенията се появи вече са известни, за да ни се отнасят за грях. защото. и TG CTG. те се използват за обозначаване на синус, косинус, допирателна и ъгъла котангенс на въртене (понякога се намери тен нотация и легло. отговорен допирателна и котангенс). От синуса на ъгъла на завъртане на 30 градуса може да се запише като sin30 °. записи TG (-24 ° 17 ') и допирателната ctgα отговарят на ъгъла на завъртане -24 градуса 17 минути и котангенс на ъгъла на завъртане α. Спомнете си, че символ ъгъл "RAD" често се пропуска Радиан мярка по време на запис. Например, косинуса на ъгъла на въртене в три пи рад обикновено означен cos3 · π.

В заключение този раздел следва да се отбележи, че в разговор за задължително, косинус, тангенс и котангенс на ъгъла на завъртане често се пропуска фразата "до ъгъла" или думата "въртене". Това означава, че вместо фразата "задължително ъгъл алфа на въртене" обикновено се използва фразата "задължително на алфа ъгъл" или дори по-кратък - "синус алфа". Същото важи и за косинус и тангенс и котангенс.

Също така, нека да кажем, че определенията на синус, косинус, тангенс и котангенс остър ъгъл в правоъгълен триъгълник са в съответствие с определения за данни, просто задължително, косинус, допирателни и ъглови котангенс на въртене стойност от 0 до 90 градуса. Това ще обясним в последния параграф на тази статия.

Следваща е необходимо, за да се отърве от ъглите и да даде определение за задължително, косинус, тангенс и котангенс брой, а не на ъгъла.

Синус, косинус, допирателна, котангенс, и т е броят на равна синус, косинус, допирателна и съответно котангенс на ъгъла на завъртане в радиани т.

Например, косинус на 8 · π по дефиниция е число, равно на косинуса на ъгъла 8 · π рад. Косинус на ъгъла 8 · π рад е равна на единица, така косинуса на 8 · π е равна на 1.

Има и друг подход за определяне на броя на синус, косинус, тангенс и котангенс. Състои се с това, че всеки реално число т се определя точка на единица кръг центриран в правоъгълна координатна система и синус, косинус, допирателната, котангенс, и определено чрез координатите на тази точка. Нека разгледаме по-подробно.

Ние показваме как да се създаде кореспонденцията между реалните числа и точките на кръга:

• 0 се определя началната точка А (1, 0);
• положително число т се определя точка от единичната окръжност, която ще получите, ако се движим в кръг от началната точка в обратна на часовниковата стрелка посока и проверете дължина на пътя на тон;
• отрицателно число т се определя точка от единичната окръжност, която ще получите, ако се движим в кръг от началната точка в посока на часовниковата стрелка и проверете дължината на пътя | т |.

Сега отиваме в определенията на синус, косинус, тангенс и котангенс на тон. Да приемем, че номер Т съответстващ на точка кръг А1 (х, у) (например, броят на пи / 2; A1 съответства на точката (0, 1)).

Sine нарича номер т ордината точка на единица кръг съответстваща на броя т. т.е. Sint = у.

Косинус на т абсциса точка нарича единица кръг съответстваща на броя т. т.е. струва = х.

Тангента т е съотношението на ординатата на абсцисата на точката на единица кръг съответстваща на броя т. т.е. TGT = Y / х. Друг еквивалентен състав на допирателната на тон - е съотношението на синуса на косинуса на този брой, т.е. TGT = Sint / цена.

Котангенс на абсцисата е съотношението на тон на ординатата на единица кръг съответстваща на броя т. т.е. ctgt = х / у. Друга формулировка е както следва: допирателна на тон - е съотношението на т косинус на синуса на тон. ctgt = разходи / Синт.

Тук ние се отбележи, че само определението на данни е в съответствие с определението, дадено в началото на този параграф. Действително, точка на единица кръг съответстваща на броя т. Това съвпада с точка резултат от началната точка завъртане под ъгъл в радиани т.

Друго е да се изясни този въпрос. Да кажем, че имаме запис Sin3. Откъде знаеш, че около синусите на 3 или ъгъл синус въртене на 3 радиани въпросните? Обикновено това е ясно от контекста, в противен случай тя вероятно не е основна ценност.

Тригонометрични функции на ъглово и числов аргумент

Според определенията в предходния параграф, всеки ъгъл на завъртане α отговарят на определена стойност на sinα. като стойността на косинус. Освен това, всички въртенето ъгли различни от 90 ° + 180 ° · к. k∈Z (π / 2 + π · к Rad) съответстват на Tg на стойности. но различен от 180 ° · к. k∈Z (π · к RAD) - стойности ctgα. Затова sinα. cosα. и tgα ctgα - е функция на ъгъла а. С други думи - това е функция на ъгловото аргумент.

По същия начин, можем да говорим за функциите синус, косинус, тангенс и котангенс на аргумента номер. В действителност, всеки реално число тон съответства на Sint определена стойност. както и разходите. В допълнение, всички числа, различни от π / 2 + π · к. k∈Z съответстват на стойностите на TGT. и броя пи · к. k∈Z - ценности ctgt.

Функциите на синус, косинус, тангенс и котангенс наречени основните тригонометричните функции.

От контекста то обикновено е ясно, с тригонометрични функции на ъглов аргумент или числов аргумент ние се занимаваме с. В противен случай, можем да предположим, че независимата променлива като мярка на ъгъла (ъглов аргумент) и числов аргумент.

Въпреки това, училището е основно проучен числови функции, т.е., функции, чиито аргументи като съответните стойности на функцията са числата. Ето защо, ако ние говорим за функции, препоръчително е да се помисли за тригонометричните функции функционира числови аргументи.

дефиниции за комуникация на геометрия и тригонометрия

Ако ние считаме, ъгълът α стойност от 0 до 90 градуса, след това данните в контекста на тригонометрията определяне задължително, косинус, тангенс и котангенс на ъгъла на въртене са в пълно съответствие с дефинициите на синус, косинус, тангенс и котангенс остър ъгъл в правоъгълен триъгълник, които са в рамките на геометрията. Нека да го докаже.

Изобразяват в правоъгълна Декартова координатна система Oxy единица кръг. Обърнете внимание на началната точка А (1, 0). това завъртане на ъгъл α стойност от 0 до 90 градуса, получаваме точка А1 (х, у). Капка от точка А1 на оста Ox перпендикулярни А1 Н.

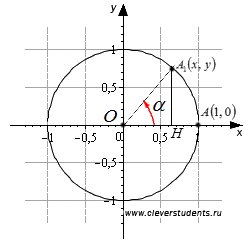
Лесно е да се види, че в правоъгълен триъгълник ъгъл А1 ОН равен на ъгъла на въртене α. дължина в непосредствена близост до този ъгъл на крака ОН равна на абсцисата точка А1. т.е. | ОН | = х. дължината на другия крак на ъгъла А1 Н А1 е равна на точката на ордината. т.е. | А1 Н | = у. OA1 и дължината на хипотенузата е равен на една, тъй като тя е радиус единица кръг. След това, чрез определяне на геометрията на задължително алфа на остър ъгъл в правоъгълен триъгълник е равна на А1 ОН противоположни отношение на крака на хипотенузата, т.е. sinα = | А1 Н | / | OA1 | = г / 1 = Y. И по дефиниция на тригонометрични задължително от а ротационните ъгъл е равен на ординатата на точка А1. т.е. sinα = у. Това показва, че определянето на задължително остър ъгъл в правоъгълен триъгълник еквивалент определяне на синуса на ъгъла на завъртане α с α от 0 до 90 градуса.

По същия начин, може да се покаже, че определянето на косинус, и допирателната котангенс остър ъгъл α съответствие с определения косинус, допирателна и котангенс ъгъла на завъртане на α.