Решението на интегралите
Интеграли и разтвор на много плаши. Да се отървем от страха, и да разберете какво е то и как да се реши интеграли!

Решението на интегралите (интеграция) е операция обратна diferentsiirovaniyu на.
За да получите по-добра представа за това, което е неразделна, ние го представя в следния вид. Представете си. Ние имаме тяло, но все още не може да го опише, ние просто знам какви елементарни частици му и как те са разположени. С цел събиране на организма в едно цяло, че е необходимо да се интегрират на елементарните частици - да се слеят части в единна система.
Геометричната форма на функция у = F (х), интеграл е областта, ограничена от формата на кривата, оста х и 2 вертикални линии х = а и х = б.
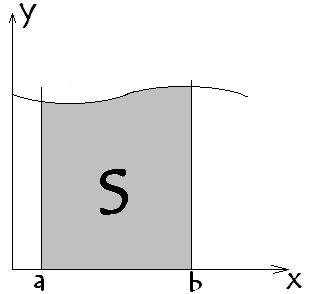
Така площта на защрихованата част е интеграл от функцията в интервала от А до точка Б.
Не вярвате ли? Ние провери на всяка функция. Обърнете прост у = 3. Ограничаване на функцията стойности а = 1, и б = 2. Построен:
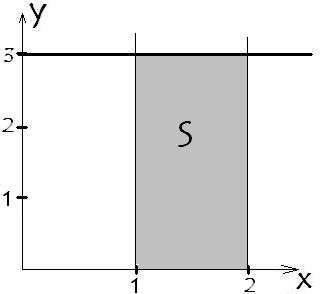
Така разбера ограничена правоъгълник. Районът е продукт на дължината от широчината. В случая, ширината една дължина 3, зона 1 * 3 = 3.
Нека се опитаме да решим едно и също нещо, без да се прибягва до изграждането с помощта на интеграцията:
Както можете да видите, че отговорът е както преди. Решение интеграли - се събират в една от някакви елементарни части. В случай на обобщи площ лента на безкрайно ширина. Интеграли могат да бъдат определени и неопределени.
Решаване на определените интеграли средства, за да се намери стойността на функцията в определени граници. Решението на неопределен интеграл се свежда до намиране на примитивна.
F (х) - примитивни. Разнообразяване на прототип, ние получите оригиналния подинтегрален. За да проверите дали интеграла решихме differentsiiruem получил отговор и сравни с оригиналния израз.
Основните функции и примитивите са дадени в таблицата, за които:
Таблица на примитиви за решаване интеграли

Основните техники на цялостни решения:
Решете неразделна средства за интегриране на функциите на променливата. Ако интеграла е с изглед на маса, може да се каже, че въпросът за това как да се реши на интеграл решен. Ако не, тогава основната задача при решаване на интеграла стане неин намаляване на оглед табличен.
Първо, вие трябва да помним, основните свойства на интеграли:
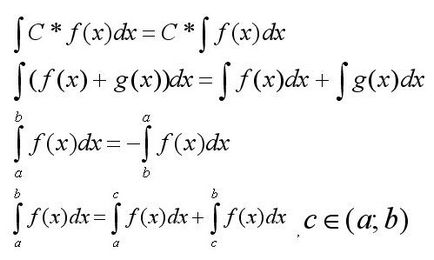
Само познаване на тези основи ще позволи да се реши прости интеграли. Но е ясно, че най-сложните и неразделна част от решението им да се прибегне до използването на допълнителни устройства. По-долу ще разгледаме някои основни примери за цялостни решения. Приеми, ще бъдат дадени за общи насоки, без примери за решения. за да не се претовари статията. Трябва да се разбере, че в рамките на 5 минути след като прочетете статията, за да разреши всички сложни интеграли не се учат, но добре оформени рамката за разбирателство, ще Ви спести часове на обучение и развитие на умения за решаване на интеграли.
Основните техники на цялостни решения
1. Промяна на променлива.
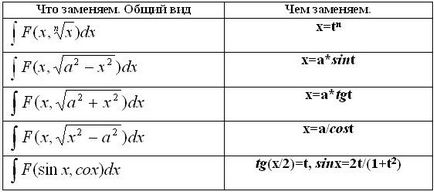
За да изпълните тази техника изисква добри умения намиране на производни.
2. Интегриране на части. Използвайте следната формула.
Прилагането на тази формула дава възможност да привидно неразрешими интеграли доведат до решение.
3. Интегриране на рационални функции.
- разлага в частични фракции
- изберете точен квадрат.
- да се създаде диференциално в знаменателя на числителя.
4. Интегриране на фракционни ирационално функции.
- изберете перфектното корен квадратен
- да се създаде диференциално в числителя на корен квадратен vyvazheniya.
5. Интегриране на тригонометрични функции.
В интеграцията на изрази
Тя се прилага формулата за продукта на разлагане.
за изразяване
т-странно, п е всяко, създаване г (cosx). Ние използваме на идентичност грях 2 + COS 2 = 1
m, п - дори, грях 2 х = (1-cos2x) / 2 и защото 2 х = (1 + cos2x) / 2
За изразяване на формата:
- Прилагане имот TG 2 х = 1/2 х COS - 1
С основни техники в тази всички. Сега се получи някакъв вид алгоритъм:
Учене решаване алгоритъм интеграли:
1. За да се разбере същността на интегралите. Необходимо е да се разбере основната същност на интеграл и неговите решения. Интеграл всъщност е сбор от елементарни части на интеграцията на обекта. Когато става въпрос за интегриране на функциите на интеграл е площта на фигурата между графиката на функцията, х-ос и границите на интеграция. Ако неопределен интеграл, т.е., са определени границите на интеграция, решението се свежда до намиране на pervobraznoy. Ако определено интеграл, е необходимо да се заменят стойностите на границите в намерената функция.
2. За да практикуват използването на таблицата на примитиви и основни свойства на интегралите. Необходимо е да се научите как да използвате таблицата на примитиви. За различни функции намерени примитиви и записани в таблицата. Ако имаме интеграл, който е в таблицата, можем да кажем, че той е решен.
3. За да разберат техниките и да получат интегралите умения за решаване. Ако интеграла не е в табличен вид, неговото решение намалява до привеждането му в под формата на таблица на интеграли. За да направите това, ние използваме основните свойства на решения и техники. Ако на някой етап на прилагането на методи, които имате трудности и неразбиране, то вие сте добре по-подробно, че е по този разписки вижте примерите за такъв план, да зададете на учителя.
В допълнение, след решението на интеграла в ранните етапи се препоръчва да се провери разтвора. За да направите това, ние differentsiiruem този израз и сравни с оригиналния интеграл.
Изпускателна подчертава няколко примера:
Примери на интегрални решения
Пример 1:
Решете интеграла:
Неопределен интеграл. Ние считаме, примитивен.
За да направите това, ние се разшири на интеграл от сумата в размер на интеграли.
Всеки от интегралите в табличен вид. Гледайте примитиви в таблицата.
цялостно решение:
Проверяваме Solution (намиране на производна):
Пример 2. решаване неразделна
Неопределен интеграл. Ние считаме, примитивен.
Сравнете с масата. Таблица №.
Разпадане използвайки свойствата това е невъзможно.
Радвайки се приеми. Най-подходящи промяна на променлива.
Замяна х + 5 т 5. т 5 = х + 5. Ние получаваме.
Dx но също така трябва да бъдат заменени от т. х = т 5-5, DX = (т 5-5) '= 5 тон 4. заместител:
Интегралът на масата. Ние считаме, че:
Заместването в отговор вместо Т,
цялостно решение:
Пример 3. Разтворът на интеграл:
За решаването на този случай, трябва да изберете точен квадрат. изберете:
В този случай koefetsient. преди неразделна резултат от заместване на DX на? * г (2х + 1). Ако установите, производните X '= 1 и? * (2x + 1) = 1, ще разберете защо.
В резултат на това сме дали неразделна табличен изглед.
Ние считаме, примитивен.
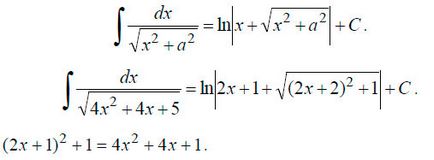
В резултат на това, ние получаваме:
Благодаря за статията, в учебниците написана като боклук! Подобно, тук пише Такео \, и тук всичко е ясно, тук всичко е решението без никакво обяснение!
Сега поне аз разбрах, че всички такива интеграли, т.е. Това е самата разбрани. А масата е много добра, пълна.
Ние в Института не са те, по дяволите neobyasnili скоро изпит в тази Noob той ми tryndit какво да правя? Защото Vyy Tipo трябва да изглежда себе си и да научи останалото зависи от вас. Аз се опитва да Istituto той се учеше, тъй като те учат там отново за неговата
Е, това е пътят към знанието, така да се каже научни изследвания. Ако искате да търсите. Възползвай се от него, да търси истината) в бъдеще, учените научават институти
Как да решим интеграла, и че по принцип те са - лесно да се разбере обяснения.
Не е ясно друго: какво толкова да се усложни решение, ако всичко е решен перфектно и без интеграли.
Вземете същия проблем с района. Ако ограничена височина област 3 (у = 3), а ширината - 1 (х = 2-1 = 1), след това разтворът с площ S = 3 * (2-1) = 3. И това е решен, се записват и се възприема много по-лесно, отколкото неразделна. И това дори не е необходимо да се изгради графика на функцията.
Това означава, че в случай на интеграла, ние произвеждаме много безполезни бележки и само, за да усложни живота си.
Изводът се предполага - интеграли ебават никой няма нужда. Бих искал да видя задачата, че би било по-лесно да се реши с помощта на интеграл от обичайния прост начин.
щеше да покаже решението на неправилни интеграли, това е основната Zapara (((
шибан! В математиката бях пълна нула.
на български език, също.
Задачата на правоъгълника е даден, за да обясни същността на интеграла. Площ на една и съща (или обем) на сложни форми без използването на интеграла просто няма да работи, за да се изчисли. В началото на тази статия показва графика на криво трапец. Така, че е възможно да се отреже кутия си и е лесно да се намери лицето й. А какво да кажем за една вълнообразна част? За точно такива неудобни поводи и неразделна употреба.
Да, и ще ви отнеме известно nevebicheskuyu функция Изградете своята графика и се изчислява площта на цифри без вградена, а аз се смея! ))))