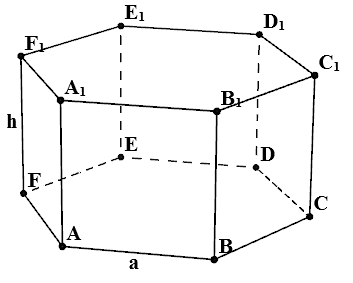
Редовен шестоъгълна призма - призма, чиято база лежат две правилен шестоъгълник и цялата страна да бъде обърната, перпендикулярна на тези основания.
наименования
- $ ABCDEFA_1B_1C_1D_1E_1F_1 $ - редовен шестоъгълна призма
- $ A $ - дължина на страната на призма основата
- $ Н $ - дължината на страничния ръб на призмата
- $ S _> $ - квадратна основа призма
- $ S _> $ - площ на страничната страна на призмата
- $ S _> $ - обща площ на призмата
- $ V _> $ - размер на Prism
Площта на призма основата
Основите на призмата редовни шестоъгълници със страни $ от $. Според свойствата на правилен шестоъгълник, квадратни призма бази е $$ S _> = \ Фрак> \ cdot а ^ 2 $$ Така се оказва, че $ s_ = S _ = \ Фрак> \ cdot а ^ 2 $.
Обща площ от призмата
Площта на призмата се състои от части на страничните повърхности на призмата и неговата базова площ. Всяка една от страничните стени на призмата е правоъгълник със страни долара на $ и $ з $. Следователно, свойствата на правоъгълника $$ S _> = а \ cdot часа $$ Y призма шест странични лица и две основи, следователно в областта на общата повърхност е $$ S _> = 6 \ cdot S _> + 2 \ cdot S _> = 6 \ cdot на \ cdot Н + 2 \ cdot \ Frac> \ cdot на ^ 2 $$
Обемът на призма
Prism обем се изчислява като продукта от площта на основата на нейната височина. Редовна височина призма е всяко едно от неговите странични ръбове, като ръб $ AA_1 $. В основата на редовен шестоъгълна призма е правилен шестоъгълник, район, известен с нас. Получават $$ V _> = S _> \ cdot AA_1 = \ Frac> \ cdot на ^ 2 \ cdot часа $$
Правилен шестоъгълник в основата на призмата
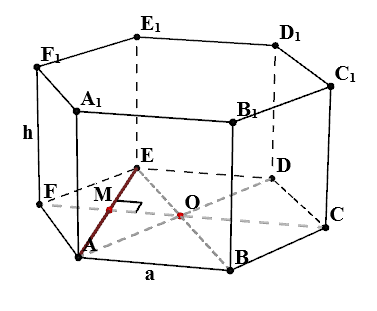
Ние считаме за правилен шестоъгълник ABCDEF, който се намира в основата на призмата. Ние прекарваме АД сегменти, BE и CF. Нека пресечната точка на тези сегменти е точката О. Според свойствата на правилен шестоъгълник, триъгълници AOB, BOC, COD, DOE, EOF, FOA са правоъгълен триъгълник. От това следва, че $$ AO = OD = ЕО = OB = СО = НА = а $$ нарязани тел на AE, пресича с CF сегмента на М. ОИО триъгълник равнобедрен, има $ AO = OE = а, \ \ ъгъл EOA = 120 $ ^. Според свойствата на равнобедрен триъгълник $$ AE = а \ cdot \ SQRT = \ SQRT \ cdot на $$ По същия начин можем да заключим, че $ AC = CE = \ SQRT \ cdot от $, $ FM = MO = \ Фрак \ cdot на $.
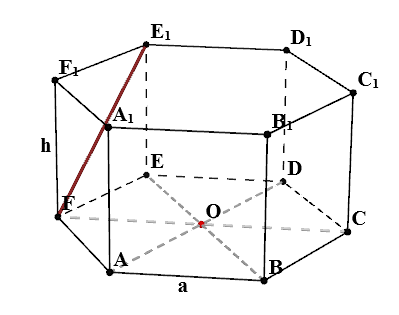
Намери $ EA_1 $
В триъгълник $ AEA_1 $ на:
- $ AA_1 = Н $
- $ AE = \ SQRT \ cdot от $ - както току-що разбрах,
- $ \ Angle EAA_1 = 90 ^ $ - свойства на редовен призма
Така се оказва, че триъгълник $ AEA_1 $ правоъгълника. Според свойствата на правоъгълен триъгълник $$ EA_1 = \ SQRT = \ SQRT $$ Ако $ H = от $, а след това $$ EA_1 = 2 \ cdot на $$ След подобни аргументи които получаваме, че $ FB_1 = AC_1 = BD_1 = CE_1 = DF_1 = \ SQRT $.
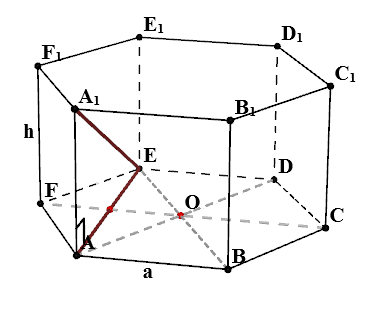
Намираме $ EB_1 $
В триъгълник $ BEB_1 $ на:
- $ BB_1 = Н $
- $ BE = 2 \ cdot от $ - защото $ ЕО = OB = от $
- $ \ Angle EBB_1 = 90 ^ $ - свойства на редовен призма
Така се оказва, че триъгълник $ BEB_1 $ правоъгълника. Според свойствата на правоъгълен триъгълник $$ EB_1 = \ SQRT = \ SQRT $$ Ако $ ч = от $, а след това $$ EB_1 = \ SQRT \ cdot на $$ се получава след подобен аргумент, че $ FC_1 = AD_1 = BE_1 = CF_1 = DA_1 = \ SQRT $.
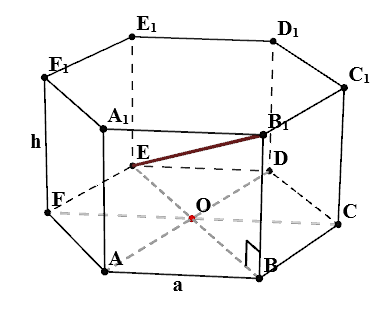
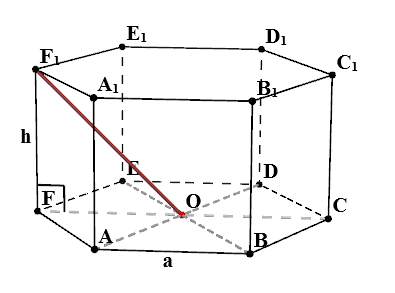
Намери $ OF_1 $
В триъгълник $ FOF_1 $ на:
- $ FF_1 = Н $
- $ FO = а $
- $ \ Angle OFF_1 = 90 ^ $ - свойства на редовен призма
Така се оказва, че триъгълник $ FOF_1 $ правоъгълни на. Според свойствата на правоъгълен триъгълник $$ OF_1 = \ SQRT = \ SQRT $$ Ако $ ч = от $, а след това $$ OF_1 = \ SQRT \ cdot на $$ се получава след подобен аргумент, че $ OA_1 = OB_1 = OC_1 = OD_1 = OE_1 = \ SQRT $.
Намери $ FE_1 $
В триъгълник $ FEE_1 $ на:
- $ EE_1 = Н $
- $ FE = а $
- $ \ Angle FEE_1 = 90 ^ $ - свойства на редовен призма
Така се оказва, че триъгълник $ FEE_1 $ правоъгълни на. Според свойствата на правоъгълен триъгълник $$ FE_1 = \ SQRT = \ SQRT $$ Ако $ ч = от $, а след това $$ FE_1 = \ SQRT \ cdot на $$ След подобни аргументи, които намираме, че дължината на диагоналите на другите странични лица на призмата също са равни на $ \ SQRT $.