Предизвикателства за геометрично доказателство за фактите на Дейтънското споразумение

Предлагам този път да се организира нещо като "доказателства маратон", за да се справи с предизвикателствата, които се предлагат във варианти ДПА девети клас по математика. Те са свързани с доказателства за проста, но в същото време много полезни геометрични факти. Статията умишлено не предостави подробна решение на проблемите, а само някои скици и съвети. Опитайте се да се преодолее този маратон от себе си, без грешки и с един замах.

Задача 1. докаже, че перпендикулярна ъглополовящата на съседните ъгли.

Ъгъл α означава една дъга, β - две

Проблем 2. два сегмента AC и BD се пресичат в една точка, която е средната точка O. всеки. Докажете равенството ACD и CAB триъгълници.

В ABCD, разбира се, е успоредник, но при условие, че това не е дадено

Доказателство: странични триъгълници са равни на двете страни и на ъгъла между тях (BO = OD - при условие, AO = OC - състояние, ∠DOC = ∠AOB - вертикален), т.е. ∠ACD = ∠CAB. И защото се лежи на кръст в пряк AB. CD и раздели AC. тогава AB е успоредна на DC. По същия начин ние доказваме успоредни линии BC и AD. Така че, ABCD - успоредник по дефиниция. BC = АД. AB = CD (в успоредник срещуположните страни са равни), AC - общо за ACD и CAB триъгълници. така че те са равни на три страни. QED.

Задача 3. показват, че средната насочва към основата на равнобедрен триъгълник, е ъглополовящата на ъгъла на противоположната субстрата, и е перпендикулярна на основата.

Ъглите, образувани от медианата и основата, се нарича "нисш", медианата и страничните стени - "горна"

Доказателство: странични триъгълници на фигурата са от три страни, от които равенството, първо, "горни" ъгли (показват, че ъглополовяща), от друга страна, "нисш" ъгли, за да се получи размер, съседен и равна на 0. 180 обаче за всеки 90 0 (показан перпендикулярност). QED.

Задача 4. Докажете, че медианата, проведено в страните на един равнобедрен триъгълник са равни.

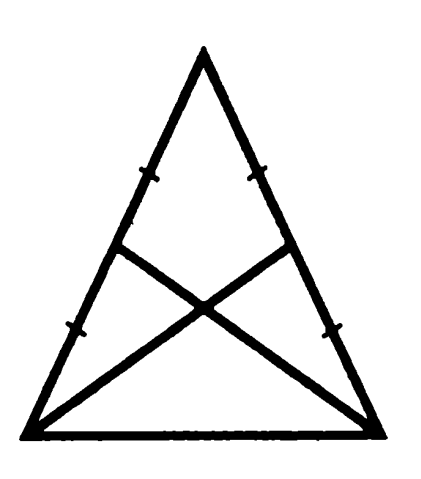
Триъгълници образувани медианите, основа и долната половини на оригиналните страни триъгълник, наречен "нисш"

Доказателство: Ъглите в основата на равнобедрен триъгълник са равни, така че "по-ниски" триъгълници са равни на двете страни и ъгълът между тях, което означава равенство проведе медиани. QED.

Задача 5. Докажете, че ъглополовящата от върха на основата на равнобедрен триъгълник са равни.

Всички ъгли са отбелязани на снимката, разбира се, равен, все пак, и са с дъги отбелязани

Доказателство: "нисш" триъгълник е равнобедрен, както следва от равенството на ъглите на дъното, "страна" триъгълници на равно страна (равно оказа по-горе частици ъглополовящи) и два ъгъла (първа равна на състоянието, последният като вертикално), така че оставащите частици ъглополовящи също равна на друг, и по този начин самите са изцяло ъглополовяща. QED.

Задача 6. Докажете, че дължината на отсечката, свързваща средата на двете страни на триъгълник е равен на половината от трета страна.

Чист страна се нарича "бази" кръстосани - "бъчви"

Доказателството: от двете страни на малки и големи триъгълника в картината се третират като 1, 2, в допълнение те имат общ ъгъл, така че те са подобни на втората черта с фактора на сходство 1, 2, и по тази причина в основата са на 1 и 2. Това QED.

Проблем 7. Докажете, че диагонала на успоредник го разделя на две равни триъгълници.

Успоредник с диагонал повече, може би, няма какво да добави

Доказателство: противоположни страни на успоредник са равни, диагонала е обща страна на тези триъгълници, така че те са равни на три страни. QED.

Проблем 8. Докажете, че средната, правоъгълен триъгълник, съставен към хипотенузата е равна на половината от хипотенузата.

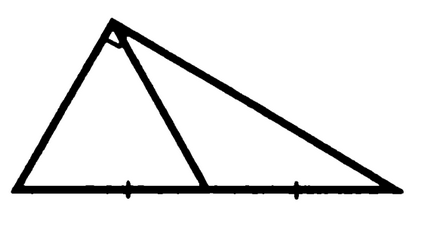
С други думи медианата, проведено от върха на правия ъгъл

Доказателство: ако около даден правоъгълен триъгълник, за да опише кръг, кръгът вписан в прав ъгъл на триъгълника ще бъде описана полукръг, така че хипотенузата е диаметърът на кръга, а половина на хипотенузата и получихме в проблема с медианата - радиуси, така че всички те са равни. QED.

Задача 9. докаже, че сегментите на допирателната към периферията на една точка, са равни.

Допълнителна строителство: свързване на точка С до точка O (психически)

Доказателството: ъглите В и линии (радиусите на кръг провежда при точката на колебание перпендикулярно на допирателната), това означава, че правоъгълен триъгълник АОС и ВОС са по хипотенузата (общо за тези странични OC въображаема контакт) и крака (окръжност с радиус OB = OA), и по този начин AC = CB. QED.

Задача 10. докаже, че диаметърът, минаваща през центъра на хордата на кръг е перпендикулярна на нея.

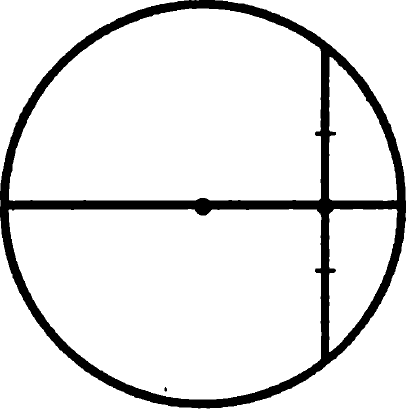
Линията, свързваща двете точки на фигурата е медианата на триъгълника, което считаме

Доказателство: В равнобедрен триъгълник, образуван от точките на пресичане на хордата с кръга и центъра на кръга е показано медианата ще бъде висока, а оттам и с диаметър, съдържащ в себе си височина, перпендикулярна на хордата. QED.

Задача 11. Покажете, че ако двата кръга имат общ акорд, линията, минаваща през центъра на тези кръгове перпендикулярна на даден акорд.

Мислено се свърже заедно всички маркирани точки на фигурата, точката на пресичане се нарича хоризонтална и вертикална посока H

Доказателството: триъгълници и O1AO2 O1BO2 са от три страни, следователно, ∠HO2A = ∠HO2B. Тогава триъгълници HAO2 и HBO2 са равни на двете страни и ъгълът между тях, а след това ∠AHO2 = ∠BHO2. и сумата на две равни ъгли може да се получи 180 0, само когато всеки от тях е 90 0. QED.

Задача 12. показват, че ако кръг може да бъде вписан четириъгълник, сумата от дължините на противоположните страни са равни.

Тангенциално четириъгълник. Наречете го ABCD. Нека M, E, X и L - допирна точка

Проблем 13. докаже, че ако някои от четириъгълник, може да бъде описан като кръг, след това сумата от неговите срещуположни ъгли са равни.

Доказателство на теоремата на вписан ъгъл сума на противоположните ъгли на четириъгълник е 180 0. заедно, тъй като те разчитат на пълен кръг, който се измерва на 360 градуса 0. QED.

Проблем 14. докаже, че ако някои от трапеца може да бъде описан като кръг, на равнобедрен трапец.

Равнобедрен трапец вписан в окръжност

Доказателство: Сумата на противоположните ъгли на четириъгълник вписан в окръжност, е α + β = 180 0 (виж задача 13.), сумата от ъглите на външната страна на трапеца също равно алфа + у = 180 0 (тези ъгли са едностранно в паралелни бази и сечащ страна страна) за сравняване на тези формули се получават че β = γ. Това означава, че от ъглите на трапец е равен, а това е наистина равнобедрен. QED.

Целева 15. В квадрат ABCD точка К и Е - средата на страни AB и AD, съответно. Докажете, че е перпендикулярна на KD CE.

Снимка на задачата

Доказателство. Правоъгълен триъгълник AKD и ECD са две Catete, така равен и всички техни елементи. нека

Сумата на ъглите в триъгълник са равни, ако, например, имат AKD триъгълник, а оттам и за триъгълника EOD има това, което е, и следователно това, което доказва, перпендикулярна KD и CE.

Доказан геометрични факти са важни, техните знания ще бъде от голяма полза за вас при решаване на по-сложни проблеми на геометрия, най-вече работни места C4 опция ЕГЕ по математика. Представено тук обясни стандартните разтвори, които трябва да бъдат поставени в изпита, разбира се, не са. Това са само насоки, като се използват които читателят ще може да се намери решение за себе си.

Във всеки случай, възможността за решаване на проблеми в геометрията е изключително важно условие за получаване на висока оценка на изпита и GIA по математика, които ще гарантират допускане до много престижни университети. Желая ти късмет в подготовката за GIA и използването, талантливи учители и късмет в изпита! Вашият преподавател Сергей V. геометрия.