Оптимално планиране 1
Проблемът, за който ние сега се обръщат към обсъждане, се нарича оптимално планиране. Удобства планиране може да бъде много по-различна система: дейността на отделно предприятие, промишлени или селскостопански, регионът, най-накрая, на държавата. Изявление на проблема за планиране е, както следва:
• Има някои цели: X, Y, и други;
• Има някои ресурси: R1 R2 и други, поради което могат да се постигнат тези цели. Тези ресурси са почти винаги ограничени;
• има определена стратегическа цел, която зависи от стойностите на X, Y, и други цели, които трябва да бъдат ориентирани планиране.
Необходимо е да се определи стойността на цели като се вземат предвид ограничените ресурси, в зависимост от постигането на стратегически цели. Това ще бъде най-добрият план.
Ето някои примери. Нека обект на планиране е детска градина. Ние се ограничим до двете целеви фигури: на броя на децата, а броят на учителите. Основните ресурси на дейностите по детските градини са с размера на финансирането, а застроената площ. Какви са стратегическите цели?
Разбира се, един от тях е за запазване и укрепване на здравето на децата. Количествена мярка за тази цел е да се намали риска от детска градина ученици.
Друг пример: планирането на икономическите дейности на държавата. Разбира се, че е твърде трудно задача за нас, за да го разбере напълно. Цели много: това е обемът на производство на различни видове промишленото и селскостопанското производство, по плана на обучение, количеството на произведената електрическа енергия, размера на заплатите на служителите в публичния сектор и др. Ресурсите включват :. Броят на населението в трудоспособна възраст, на държавния бюджет, природни ресурси, енергия, възможността за транспортни системи и т.н. Както можете да си представите, всеки един от тези видове ресурси са ограничени. В допълнение, най-важният ресурс е времето, отделено за изпълнение на плана. Въпросът на стратегическите цели по-скоро сложно. Държавата има много от тях, но в различни периоди от историята на приоритетите на целите може да варира.
Ако искате да използвате компютър, за да се реши проблема с оптимално планиране, ние отново трябва да се изгради математически модел. Затова всичко, което е казано в началото на този раздел, трябва да бъде преведена на езика на числата, формули, уравнения, както и други средства за математика. В своята цялост, тази задача е много трудно за реални системи. Както и преди, ние приемаме по пътя на опростяване.
Помислете за един много прост пример, от който можете да получите представа за един подход за решаване на проблема с оптимално планиране.
Пример. Училище сладкарница подготвя баници и сладкиши. Поради лимитирания капацитет за съхранение на ден, можете да се готви в не агрегат повече от 700 продукти. Работен ден в сладкарски магазин трае 8 часа. Ако проблемът само торти, денят може да се направи не повече от 250 парчета от пая можете да направите 1000, ако тя не произвежда торти. Цената на тортата е два пъти по-висока от Пати. Необходимо е да се направи всеки ден на производствения план, което осигурява сладкарница най-много приходи.
Разбира се, това е чисто казус. Малко вероятно е, че има сладкарница, която произвежда само два вида продукти и едва ли е най-голям приход - целта на работата му. Ние работим от математически модел на проблема.
са Target:
х - ден пайове пътна карта;
в - ден торти пътна карта.
В този пример може да се нарече производствени ресурси? От факта, както е посочено в отчета за проблем е:
продължителността на работния ден - 8 часа;
складиране капацитет - 700 легла.
Предполага се, че за улеснение на други ресурси (суровини, електроенергия и др.), Които не са ограничени. Сформиране на цели - постигане на максимална отдела за приходите - ще обсъдим по-късно.
Снабдете отношения, на следните условия на ограничения във времето, за работилница и склад капацитет, т.е. общият брой на статии.
От условията на проблема, от това следва, че за производството на сладкарски изделия, прекарано 4 пъти по-дълго от направата на пай. Ако ние означаваме производство пай - т мин, времето за производство ще бъде равна на 4т торта минути. Така че, общото време на баници и сладкиши на производителя е:
TH + 4ty = (х + 4Y) т.
Но този път не може да бъде по-дълъг от срока на действие на работен ден. Това следва от неравенството
Лесно е да се изчисли тона - по време на конструкцията от пая. Що се отнася до времето на 1000 броя може да се направи, а след това една пирожка прекарал 480/1000 = 0.48 мин. Заместването на тази стойност в неравенството, ние получаваме;
(X + 4Y) · 0.48 <= 480.
Ограничение на броя на продуктите дава съвсем очевидно неравенство:
Двамата получиха неравенства трябва да добавят термини положителни стойности на х и у (не може да бъде отрицателно число на баници и сладкиши). В резултат на това получаваме система на неравенството:
И сега за формализирането на стратегическите цели: увеличаване на приходите. Приходи - е стойността на всички продукти, продавани. Да предположим, че цената на един пай - Р рубли. Според проблема, цената на тортата два пъти, т.е. 2r рубли.
Ние ще разгледа писменото изразяване, като функция на х, у:
Тя се нарича целева функция.
Тъй като стойността на R - константа, максималната стойност на е (х, у) се достига при максималната стойност на (х + 2y). Поради това, както целевата функция може да се приема:
е (х, у) = х + 2y.
Следователно, за да се получи оптимален план свежда до следното математическо проблема: да се намери цели стойност на х и у удовлетворяват неравенството в системата ". при които целевата функция "се максималната стойност.
По този начин, на математическия модел на оптимално планиране на сладкарница училище построена.
Математическа дисциплина, която е посветена на решаването на такива проблеми, наречен математически програмиране. Тъй цел функция F за (х, у) на х и у са линейно (т.е., в първа степен), ни проблем се отнася до частта от тази наука нарича линейно програмиране.
Система на неравенството, написани по-горе се появява на четириъгълника координатната равнина. ограничена от четири прави линии, съответстващи на линейните уравнения:
х + у = 700;
х = 0 (у-ос);
Фиг. 2.19, тази област е четириъгълник ABCD и подчерта запълни. Всяка точка на четириъгълник е разтворът на система от неравенства. Например, такава точка е точка с координатите х = 200, у = 100. Това съответства на стойността на обективната функция F на (200,100) - 400. Точка х = 600, у = 50 съответства
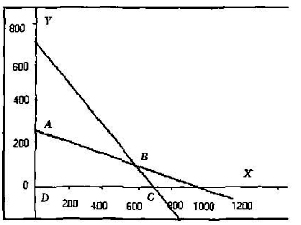
Фиг. 2.19. Площ търсене на оптимален план
F (600,50) = 700. Но, очевидно, желаният разтвор е ABCD точката на една област, в която се максимизира обективната функция. Намирането на този етап се извършва с помощта на линейни методи за програмиране.
Тези практики са в MS Excel математически арсенал в следващия раздел ще научите как да ги използвате.
Най-важните характеристики
Оптимално планиране е да се идентифицират цели стойности имат предвид ограничените ресурси, в зависимост от постигането на стратегическата цел.
ограничени ресурси математически представени като система от неравенства.
Формализирането на стратегическите цели намалява с изграждането на целевата функция и целта на определени условия за неговото величина, най-често се постигат максимална или минимална.
Математическо програмиране - клон на математиката, съдържащ методи за решаване на проблеми на оптимално планиране.
Линейно програмиране - клон на математическото програмиране, решаване на оптимално планиране проблем с линейна целева функция.
Въпроси и задачи
1. а) Какъв е проблемът на оптимално планиране?
б) Какви са целите, средствата, стратегическа цел? Дайте примери.
б) Каква е математическо програмиране, линейното програмиране?
3.а) Формулиране на проблема за оптимално планиране на същата DLL училище сладкарница, която произвежда три вида продукти: баници, сладкиши и бисквити.
б) направи промяна в състава на оптимално планиране на нишките 17 за два вида продукти, които отговарят дори една условия ограничение: броят на торти трябва да бъде не по-малко от броя на пайове. На координатната равнина, изграждане решение вашето търсене.
Semakin IG Henner EK Компютри и ИКТ, 11
Изпратено от читателите на уебсайтовете
Ако имате корекции или предложения на този урок, моля свържете се с нас.
Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.