Най-простият от първи ред диференциални уравнения, примери, разтвори

В тази статия ще се занимава с решаването на най-простите от първи ред диференциални уравнения, които не съдържат неизвестната функция ш. Такива диференциални уравнения са или вече решени за производно, или те могат да бъдат разделени по отношение на производно.

Общият разтвор на диференциални уравнения на формуляра в предварително определен интервал X може да се намери чрез интегриране на двете страни на това уравнение. Ние се получи. Ако се обърнем към свойствата на неопределен интеграл. след това се стигне до желания общия разтвор Y = F (х) + С, където F (х) - един от F на примитиви функция (X) в X. интервала и С - е произволна константа.

Имайте предвид, че обхватът на X не е показана в много проблеми. В този случай това означава, че трябва да се търси решение на всички х. и в която неизвестен функция у. и оригиналното уравнение има смисъл.

Ако искате да намерите конкретно решение на диференциално уравнение, което отговаря на първоначалното състояние ш (x0) = y0. след намирането на общо интеграл на у = F (х) + С все още трябва да се изчисли стойността на константата С = С0. Използването на първоначалното състояние. Това означава, че константата С = C0 се определя от уравнението F (x0) + С = Y0. и желания специално диференциално уравнение е форма у = F (х) + C0. Помислете за пример.

Намерете общото решение на диференциално уравнение, проверка на коректността на резултата. Намери конкретно решение на уравнението задоволяване на началните условия.

Интегриране на първоначалната диференциално уравнение, ние получаваме. Това неделима вземе метода на интегриране по части:

Така, - общото решение на диференциално уравнение.

За да се провери точността на резултата от проверката. За тази получения разтвор да замени оригиналния уравнение:

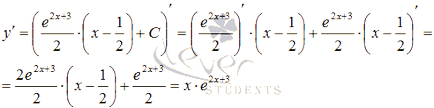
Ето защо, когато първоначалното уравнение става за самоличност, така че общото решение на диференциалното уравнение намери правилно.

Трябва да се отбележи, че намереното решение е общото решение на диференциално уравнение за всички валидни стойности на аргумента х.

Остава да се определи конкретно решение на ОДУ с първоначално състояние. С други думи, трябва да се намери стойността на константи C, на която ще бъде истинско равенство.

Следователно, замествайки С = 2 в общото решение на ТАС получи конкретен разтвор на диференциално уравнение, което отговаря на предварително определено начално състояние.

Обикновено диференциално уравнение може да бъде решен за производно, се раздели двете страни е (х). Такава трансформация ще бъде еквивалентен ако е (х) не е равно на нула по всяко х в интервала на интеграция на X. диференциално уравнение

Може да има случаи, когато и да премине към нула за определени стойности на аргумент х ∈ X функция F на (X) и г (х). За такива стойности на х общото решение на диференциално уравнение е функция на база. дефинирани като ги.

Ако аргументът за някои х ∈ X стойности на условията, а след това одата още няма решения.

За интервал Х X общ разтвор на диференциално уравнение на покой се определя от уравнението преобразувания. Нека разгледаме следните примери.

Намерете общото решение на обикновено диференциално уравнение.

Тъй като ние знаем основните свойства на елементарни функции, които естествен логаритъм функция определени за положителни стойности на аргумента, обаче домейн на функция у = LN (х + 3) е интервалът х> -3. Следователно, първоначалното диференциално уравнение има значение за х> -3. При тези стойности на експресия аргумент х + 3 не става нула, следователно, може да бъде решен за производно ОДУ раздели двете страни от х + 3 получава.

Сега ние трябва да се интегрират получените диференциални уравнения решени за производната :. За да приемате това неразделна ние използваме метода на още свързване на знак от разликата. , Така, - общото решение на диференциално уравнение за х> -3.

Вижте всички решения на диференциалното уравнение.

Уравнението на диференциално има смисъл за всички недвижими х. Ако приемем, че х ≠ 0. то може да се превърне формата на ОДУ. Когато х = 0 изходния уравнението става идентичност за всички функции, определени при х = 0. По този начин, когато х = 0 разтвор на диференциално уравнение е функция на база. определен на нула аргумент.

Ние интегрираме диференциалното уравнение:

- диференциално уравнение, когато х = 0 разтвор на диференциално уравнение е функция, определена за тази стойност на аргумента.

Намерете общото решение на обикновено диференциално уравнение.

sinx изчезва за. Към тези аргументи cosx ≠ 0. Следователно, стойността на първоначалната диференциално уравнение няма решение. В този случай, можем да разделим двете страни от sinx. Ние получи одата решен за деривата. то Интегриране :. Така, - общото решение на диференциално уравнение.

• Èl'sgol'ts LE Диференциални уравнения и смятане на варианти.