Линейна алгебра матрица

инверсната матрица 13

Място на 16

Linear Независимост 21

Система от линейни уравнения 24

Методи за решаване на системи линейни уравнения 27

27, методът на обратен матрица

Метод за решаване на системи линейни уравнения с квадратна матрица от правило Cramer на 29

Гаус "метод (Метод последователни елиминиране на променливите) 31

Razmeramhn- матрица е правоъгълна маса на номера, soderzhaschayamstrok instolbtsov. Числата, които изграждат масива, наречени елементи на матрицата.

Матрици обикновено са обозначени с главни латински букви, както и елементи - същото, но с малки букви с двойно индексиране.

Например да разгледаме матрица А измерение 2 х 3:

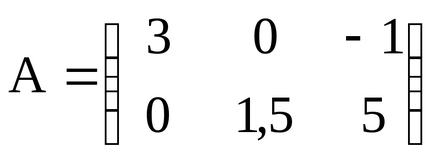
В тази матрица на два реда (т = 2) и три колони (п = 3), т.е. Тя се състои от шест elementovaij. gdei- номер на ред, к - брой на колоната. В този случай е необходимо стойности от 1 до 2 и от един до три (записани

). А именно, a11 = 3; a12 = 0; a13 = 1; a21 = 0; А22 = 1,5; А23 = 5.

матрици А и В са същите размери (М х N) nazyvayutravnymi. ако те са едни и същи елемент от елемент, t.e.aij = BIJ за

, т.е. за lyubyhiij (може zapisati, й).

Matrix-низ - матрица, състояща се от един ред, колона amatritsa - матрица, състояща се от една колона.

Например, - един ред матрица, и

.

Квадратна матрица на п-тия ред - матрица в брой е равен на броя на редовете и колоните е равно на п.

Например,

- втори ред квадратна матрица.

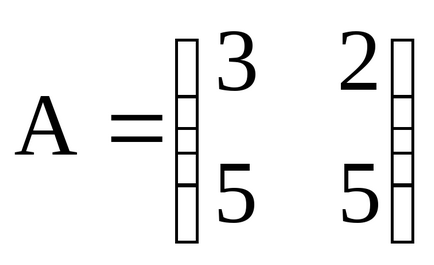
Диагоналните елементи на матрицата - елементите, чиито ред брой е равен на броя на колоната (Aij, J = J). Тези елементи obrazuyutglavnuyu диагонална матрица. В предишния пример, основната форма диагонал elementya11 = 3 5 = ia22.

Диагоналната матрица - квадратна матрица, при което всички извън диагонал елементи са равни на нула. Например,

- диагонална матрица на третия ред. Ако всички диагонални елементи са равни на един, след това nazyvaetsyaedinichnoy матрицата (обикновено означен с буквата Е). Например,- третият ред единица матрица.

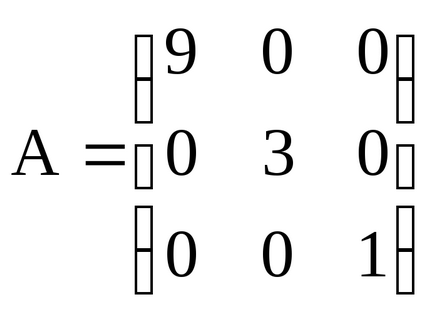
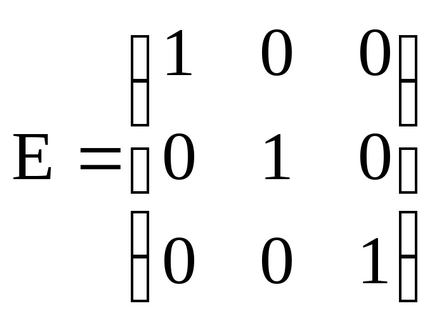
Матрица се нарича нула. ако всички негови елементи са нула.

На квадратен матрицата се нарича триъгълен. ако всички елементи по-долу (или повече) на главния диагонал са равни на нула. Например,

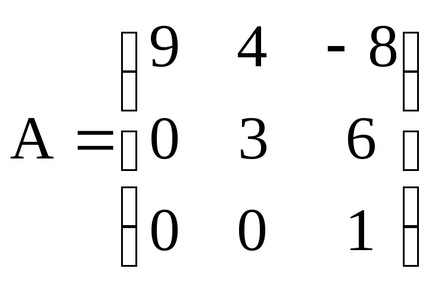
- триъгълна матрица на третия ред.

Манипулиране на матрици

На матрици може да изпълнява следните действия:

1. Размножаване на матрица от редица. Продуктът от матрицата на матрични В = chislonazyvaetsya A елементи kotoroybij = aij за lyubyhiij.

Например, ако

, на.

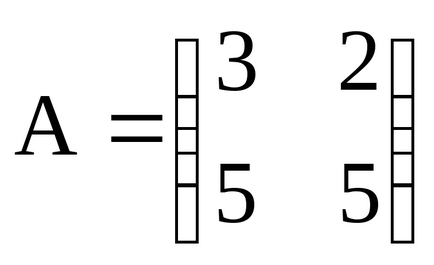
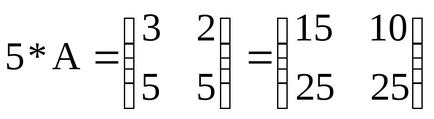
2. Добавяне на матрици. Сумата от две матрици А и Б от еднакъв размер m х п е матрицата С = A + B, чиито елементи Сий = Aij + BIJ dlyai, к.

Например, ако

на

.

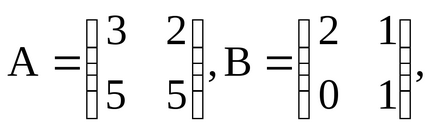
Отбележете, че в предишната операция може да се определи изваждане матрици със същия размер: разликата А-В = A + (-1) * Б.

3. умножение на матрици. Продуктът на матрицата А razmeramxnna razmeranxpnazyvaetsya матрица В е матрица С, всеки елемент Сий е равен на сумата от продуктите на елементи и-ти ред на матрицата, съответстващи на elementyj-тата колона на матрицата В, т.е. ..

, Размерът на матрицата продукт е 2 х 3, и ще има формата:

В този случай, матрицата е съгласуван с W. матрицата

Въз основа на работата на умножение за квадратни матрици, определени за работа степенуване. Една степен на положително цяло число m (т> 1) на квадратна матрица М на матрици, е продуктът, равна на А, т.е.

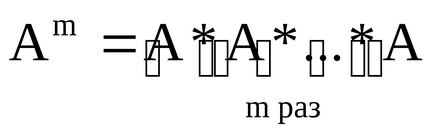
Ще подчертая, че добавянето (изваждане) и умножение на матрици не е определен за всеки две матрици, но само за да отговори на специфичните изисквания на своето измерение. За намирането на сумата или разликата от размера на матрицата трябва да бъде същото. За да намерите броя на колоните на матрицата продукт на първата от тях трябва да съответства на броя на вторите линии (като последователна матрица се нарича).

Помислете за някои от свойствата на които се считат като аналогична на свойствата на операции на номера.

1) е комутативен (комутативен) Освен закон:

2) асоциативен (асоциативен) право на добавка:

(А + В) + C = A + (В + С)

3) Разпределението (разпределение), правото на умножение над допълнение:

5) асоциативен (асоциативен) закон за умножение:

Ще подчертая, че комутативен закон на умножение на матрици като цяло не е удовлетворена, т.е. AB BA. Освен това, наличието на AB не означава непременно наличието на VA (матрицата не може да бъде последователно, и след това им продукт обикновено не се определя, както в горния пример за матрица умножение). Но дори и да не съществуват и двата продукта, те са обикновено по-различно.

В конкретния случай на комутативен право продукт или е квадратна матрица А от матрицата на идентичност на същата последователност, и този продукт е равна на А (размножаването на идентичност матрица е подобен на умножаване единица при номера на умножение):

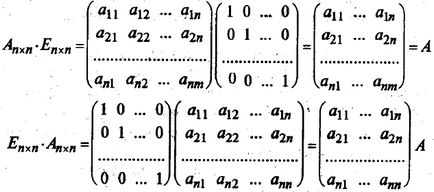
Ще подчертая още една разлика умножение на матрици от умножаване на числа. Каталог на числата може да бъде нула, ако и само ако поне един от тях е нула. На матрици, които може да се каже, че продукт на ненулев матрица може да бъде равна на нула матрица. Например,

Продължаваме разглеждането на матрични операции.

4. Въвеждане матрица е преход работа на матрицата A T A razmeramxnk razmeranxm матрица, в която са разменени редове и колони:

%.

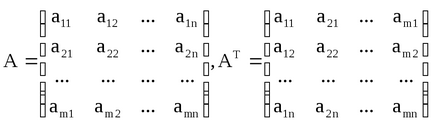
Имоти транспонират работа:

1) От дефиницията следва, че ако матрицата транспониране два пъти, се върнем към първоначалната матрица: (А Т) Т = А.

2) постоянен фактор могат да бъдат взети извън транспониране (A) ​​Т = Т A.

3) Въвеждане разпределителни по отношение на събиране и умножение на матрици: (AB) T = В T A T и (А + В) T = В T + A Т.