Косинус и задължително как да се реши

За решаването на прости тригонометрични неравенства. , , (Вместо на етикета може да е ..) се използват, графичен начин. Виж точката на пресичане на графиката със съответната функция линия. разположен по-близо до произхода, а след това се използва периодичността на функцията.

При по-сложни тригонометрични неравенства намалена до най-простата си случай посредством опростяване.

Графики и основните свойства на тригонометричните функции.

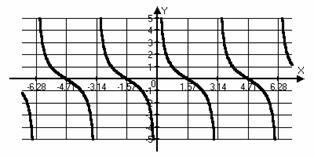
Графики и основните свойства на обратни тригонометрични функции.

Функция или дори, или нечетен

Функция или дори, или нечетен

Съобщение тригонометрични функции на обратните тригонометрични функции, извършвани от таблицата по-долу

По този начин стойността на експресията 0.

Обяснение на раздел: Решение на тригонометрични уравнения и неравенства.

За решаването на произволни тригонометрични уравнения и неравенства прилагат същите основни техники, които са описани по-горе за решаване на алгебрични уравнения: въвеждане на нова променлива и факторинг лявата страна на уравнение или неравенството.

От общите съображения, се посочва следното: замяна на една друга функция, за да се избегне въвеждането на радикали, тъй като това усложнява решение и изисква проверка на корени намерени (в изграждането на уравнението на властта могат да се появят странични корени).

Понякога е възможно, прехвърляне на всички условия към лявата страна на уравнението, тя се разпространи върху факторите.

1. Уравнения и относително хомогенен.

Всяка от уравнения:

и е хомогенен по отношение. Сумата на експонентите у и всички членове на едно уравнение. Това количество се нарича степента на хомогенна уравнение. Разделяне с. степента на хомогенна уравнение, може да се редуцира до уравнение по отношение на алгебрични.

Разделяне, например, на уравнение. получаваме уравнението:

Когато тези уравнения са еквивалентни, като че ли. след първото уравнение получаваме това. че е невъзможно (и същия аргумент не изчезват). На следващо място, от еквивалентно уравнение намираме. решаването на квадратно уравнение. и на ценностите - съответните стойности.

4. Решете уравнението:

Решение. И замяна. Ние получи хомогенна уравнение:

Въвеждаме нова променлива, а ние се получи квадратно уравнение за него:

Корените на това уравнение. На следващо място, ние се равностоен набор от уравнения:

2. уравнения, от лявата страна на който се разделят на фактори, а от дясната страна е нула.

Прехвърляне на всички условия на всяко уравнение в лявата страна, тя може да бъде намалена до формата.

Ако лявата страна на това уравнение се разлага на фактори, като всеки от тях е равен на нула, а уравнението се разпада на няколко прости уравнения. Важно е да се има предвид, че корените на оригиналното уравнение са само тези, от корени на уравнения, получени, които попадат в рамките на домейна на оригиналното уравнение.

5. Решете уравнението:

Решение. Ето защо е препоръчително да се използват формулите за преобразуване на тригонометрични функции работи в количество. С помощта на тези формули, получаваме уравнението:

косинус Разликата превърне в един продукт. което е еквивалентно на снимачната площадка на уравнения:

Тези уравнения могат да бъдат решени с помощта на тригонометрични смяна универсален. използване на формули и изразяване чрез.

Оригиналният уравнение се свежда до един рационален алгебрични уравнения, решаването на които преди това са обсъждани.

Тези уравнения са решени чрез въвеждане на по-рационално спомагателни ъгъл :. Да разгледаме по-нататъшния ход на решаване на уравнението чрез еквивалентни трансформации отляво:

Имайте предвид, че изразът в скоби в този случай се превръща в един косинус от разликата от аргументите:

По този начин, на оригиналния уравнение е еквивалентно на простата тригонометрични уравнение:

разтворът от които са

Проблемът е решен в обща форма.

6. решаване на уравнението:

Въвеждаме нова променлива, и се получи еквивалентен квадратно уравнение.

в която дискриминантата е нула и, следователно, има един корен. Проблемът се свежда до решаване на уравнението:

Решение. (Втори метод). Представяме спомагателната ъгъл :.

След решението на оригиналното уравнение веднъж в писмена форма:

С други думи, ние имаме един и същ отговор, което не е изненадващо.