Как да си намерим страна правоъгълен триъгълник

Ние казваме, че тези компоненти (стени, ъгли и т.н.) да определи фигурата ясно, ако друга фигура с едни и същи компоненти непременно равни на оригинала. Например, за двете страни на триъгълника и ъгълът между тях, и две странични съседни него ъгъл или три страни на основата на равенство на триъгълници определя еднозначно всеки триъгълник. Има и други случаи, недвусмислено определяне триъгълник е равнобедрен триъгълник с базата данни и се спуска по височина, триъгълници на тези три медиани на триъгълника на данни от три височини и т.н. Това е много важно за решаване на проблема за определяне на планиметражна Фигурата ясно продължи да се намери, че нейните неизвестни компоненти, които са необходими за продължаване на процеса на решаване на проблема.

За да намерите най-непознати страни и ъгли на триъгълник е уникално определени обикновено използват теоремата на Синиш и уют.
@

където R - радиус приблизително триъгълник okruzhnosti.Teorema уют

Оказва се, че при определяне на ъгъла на триъгълника е най-добре да се намери косинуса от синусите. Това се дължи на факта, че синуса не прави разлика между съседни ъгли: Косинус отличава всички ъгли от 0 до стр. където остри ъгли да е положителна за прав ъгъл - е равна на нула, а тъпият ъгъл - отрицателни, както и:.

Следният пример илюстрира прилагането на задължително и косинус теорема за намиране на неизвестните страни и ъгли на някои от уникалните триъгълници. Направи свой собствен.

Отговор: а). , G = р - а - б;

б). , В = р - г - а;

@ Като правило, при решаване на триъгълници първо се стреми да определи три страни, и след това се намери необходимите компоненти. С известни трите страни на триъгълника, за да по-точно рисуване умалено изображение, трябва да може да се определи вида на триъгълника (на остроъгълен, правоъгълен или тъп).

Формулата резултат от косинус теорема прилага в най-голяма ъгъл, предвид знака на косинус, може да се получи връзка между страните на квадрата, което позволява да се определи формата на триъгълник.

Вследствие на триъгълник, в който в - най-голямата партия, е тъп, ако; остроъгълен ако и когато правоъгълна.

Упражнение 6 .2.2.

По дължината на трите страни на триъгълника, за да се определи вида:

Забележка. Известно е, че срещу по-голямата страна на триъгълника е по-голям ъгъл, и обратно. Косинусна голям ъгъл може да се намери от формула следната теоремата на уют.

Отговор: а) и б) правоъгълна, б) тъп, г) остроъгълен и т.н.) не съществува.

Във връзка с упражняването 6.2.2. г) трябва да се отбележи доста често се прилага при решаването на геометрични проблеми т.нар триъгълник неравенство. @ Три сегмента могат да образуват триъгълник, ако и само ако сумата от дължините на по-малките по-дълги от по-голям.

Още един друг вариант на изпълнение на състава се използва неравенството триъгълник: За всеки три точки А, В и С имат з AB - BC AC chЈ J AB + BC; където дясното неравенство се превръща в равенство, само когато точка Б се намира на отсечката AC; и лявата неравенството между половете става само когато точките А, В и С са линейните и точка Б, не се съдържат в сегмента AC.

Сега ви представяме примери за решаване на някои задачи в кандидатстудентски изпити Кубан държавен университет.

Въз основа на AC ABC триъгълник. Това конструирана като диаметър кръг, който пресича страни AB и BC в точките М и N, съответно. Намерете радиуса на кръга, ако AB = а и AM = а. И CN = б. решение

От равнобедрен триъгълник АОМ намери P А = (р - а) / 2. равнобедрен триъгълник и от CON находка P C = (р - б) / 2. защо P B = р - П А - П С = (А + В) / 2.

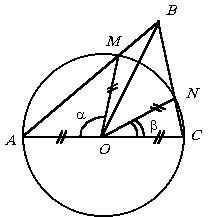
Значение намиране на ъгли А и В се крие във факта, че триъгълника ABC, ние ще знаем страна AB = A и две съседни, за да му ъгъл, т.е. D ABC е еднозначно решен. Остава да се намери неизвестен страна AC както в примера в точка 6.2.1): и. Където радиусът на кръга е.

Пример 6.2.4. (Кубан държавен университет, математика. 1979)

В триъгълник ABC вписан кръг. Точки D, Е, F - точка на допиране страни AB, BC, CA, съответно. Определя се площта на триъгълник ABC. ако AB = A, BC = б, R ДЕФ = 60 °.

Тази референтна Интересно е това, че D ABC съгласно мотиви долу ще се определя еднозначно. Въпреки това, с тези компоненти може да има не повече от два различни триъгълници! решение

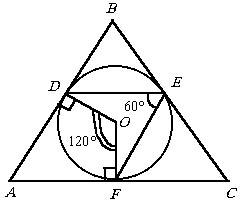
Нека O - център на вписан кръг. Тъй DEF вписан ъгъл е 60 °. DOF централния ъгъл е 120 °. Сборът от ъглите на четириъгълник ADOF равна на 360 °. Така че ние знаем за триъгълника ABC, двете си страни AB = а, BC = б. и ъгъл (не е между тях!).

На следващо място, ние се стремим да намерим трета страна AC. Ако приемем, че AC = х, ние имаме уют и теорема. Местоположение. След това ние откриваме площта на триъгълника ABC формула.
Отговорът е двусмислен!

Забележка. Препоръчително е да не се ограничава до отговора в решаването на предходната проблема.

Така че, ако, (т.е.), проблемът няма решение.

Ако същата или б> а. (Т.е. и двете), тогава проблемът има уникален разтвор :.

Едва когато (че) ние показахме по-рано двуцифрена възвращаемост.

Сега, за прилагането на неравенство на триъгълника илюстрации представят решаването на проста задача устни изпити по математика факултет на Кубан държавен университет.

Докажете, че сборът от двете медианите на триъгълник е по-малко от своя периметър. доказателства

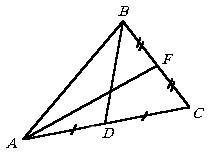
От неравенството триъгълник на D ABF и D ACF имат AF

Когато по аналогичен начин от D АБД и D CBD. 2 BD получи <, а значит 2AF + 2 BD <2 и AF + BD <. что и требовалось доказать.

Докажете, че всеки триъгълник ABC Г. всяка точка лежи вътре в нея или на една страна, дължината на сегмент е по-малко от АД semiperimeter триъгълник ABC.

Забележка: Използвайте аргументи, подобни на тези, дадени в началото на доказателството за предишната работа.

В заключение този раздел ще представи три типични задачи, решения, при които основната роля на теоремата за уют.

За да илюстрираме реши а).

а) Като се има предвид: А, В, С, D. Намерете е.

б) Като се има предвид: а, б, в, г. Намери г.

в) Като се има предвид: A, C, D, F. Намери б.

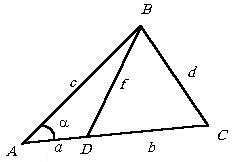
Ние въведе допълнително Р А = а. От D ABC находка
.
Тогава от D ABD намери.
т.е. ,

Задачи б) и в), за да вземе решение за себе си. Имайте предвид, че при решаването на б), както и в а), може да бъде само една стойност за сегмента на неизвестен дължина, и работата в) два възможни желаните стойности за б.

НАПРЕД | Назад | НАЧАЛО | планиметрия | стереометрия