Как да се реши проблема на квадратна функция

Отговор :. нули «у = х с 2 - 3" X1 = √ 3; х2 = - √ 3.

Как да се намери за какво стойности на «х» квадратна функция е на числова стойност

За да разберете за какво стойности на «х» квадратна функция приема предварително определена числова стойност, трябва да:

• вместо «у» заместител в зависимост от предварително определена числова стойност;
• решаване на полученото квадратно уравнение «х».

За което стойностите на «х» функция «у = х 2 - х - 3" се стойността "-3".

Ние замени първоначално функция «Y = х 2 - х - 3" вместо "у = -3» и да намерят «х».

у = х 2 - х - 3

-3 = х 2 - х - 3
х 2 - х - 3 = -3
х 2 - х - 3 + 3 = 0
х 2 - х = 0
x1 2 =

1 ± √ 1 с 2 - 4 · 1 · 0

Отговор: «х = 0" и "х = 1" функция «у = х 2 - х - 3" е на стойност «ш = -3».

Как да намерите координатите на параболата и линията на точки на пресичане

За да намерите точката на пресичане на парабола с Необходима е реда:

• което се равнява на дясната страна на функциите (функции на тези части, които съдържат «х");
• решаване на полученото уравнение за «х»;
• Заместването на числовите стойности «х» в някоя от функциите, както и да намерите координатите на точки по оста "Oy".

Намерете координатите на точките на пресичане на парабола «у = х 2" и директен «у = 3 - 2x».

Приравняването на дясната страна на функции и решаване на полученото уравнение за «х».

2 = х 3 - 2х
х с 2 - 3 + 2x = 0
х 2 + 2х - 3 = 0
x1 2 =

2 ± √ 2 с 2 - 4 · 1 + (-3)

Сега замести всеки от предварително определени функции (например, «у = 3 - 2х»), получен цифровата стойност "X", да намерите координатите «г» пресечните точки.

1) х = 3
у = 3 - 2х
у (3) = 3 - 3 = 2 х 3-6 = -3
(·) А (3, 3) - първата точка на пресичане.

2) X = -1
у = 3 - 2х
Y (-1) = 2 - 3 · (-1) = 3 + 2 = 5
(·) B (1; 5), - втората точка на пресичане.

Запишете пресечната точка с координати в отговор.

Отговор: «Y = х 2" точки на пресичане на парабола и една права линия «у = 3 - 2x»:
(·) А (3, -3) и (·) B (1; 5).

Как да се определи дали дадена точка на функцията на парабола графика принадлежи

За удостоверяване на собствеността върху точката на параболата не е необходимо да се изгради графика на функцията.

Достатъчно е да се замени координати на точката на формула функция (координата на «Ox» ос вместо «х», и координатите на «Oy» ос вместо «ш») и извършване на изчисления аритметика.

• Ако получите истинско равенство, това означава, че точката принадлежи на графиката на функцията.
• Ако получите грешен паритета, точката не принадлежи на функцията график.

Не система «у = х 2" на графиката, се определи кои точки са част от него: (+) A (2, 6). (·) B (1; 1).

Заместител в функция «у = х 2" координатите на точка (+) (2, 6).

у = х 2
6 = 02 Февруари
6 = 4 (неправилно)

Така, точка (+) А на (2; 6) не принадлежи към графиката на «у = х 2".

Заместител в функция «у = х 2" координира точки (·) B (1; 1).

у = х 2
1 = (-) 01 Февруари
1 = 1 (истина)

Следователно, точка (·) В (1; 1) принадлежи към графиката на «у = х 2".

Как да се намери точката на пресичане на парабола с координатните оси

Виж координатите на точките на пресичане на парабола «у = х 2 -3x + 2" на координатните оси.

Първо ние определяме функция точка на пресичане с «Вол» ос. На графиката на точките са както следва:

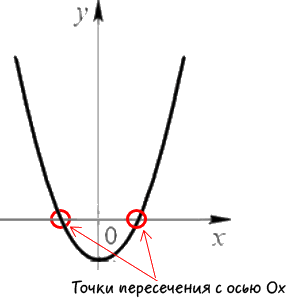
Както е показано на фигурата по-горе, координатите «у» към «Вол» ос пресечни точки е нула, така че можем да замени «у = 0" в първоначалната функция «Y = х 2 -3x + 2" и да намерят своя координати «Вол» ос.

0 = х 2 + 2 -3x
-3x + 2 х 2 = 0
x1 2 =

± √ 3 3 с 2 - 4 · 1 · 2

Ние напиши генерираните координатите на пресечните точки с «Ox» ос: (·) A (2, 0) и (·) В (1, 0).

Сега ние намираме координатите на точката на пресичане с оста Oy «».

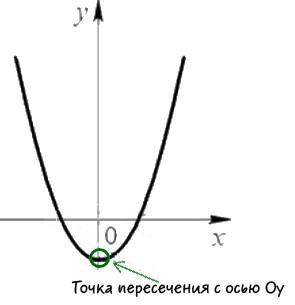
Както е показано на фигурата по-горе, координатите «х» пресичане с «Oy» ос е нула.

Заместването «х = 0 'в оригиналната функция« Y = х 2 -3x + 2 "и да се намери точка координира на« Oy »ос.

Y (0) = 0 2 - 3 х 0 + 2 = 2

Добави от координатите на точка получен: (·) C (0, 2)

Пишем в отговор на всички координатите на пресечните точки на осите параболата.

Отговор: «Ox» пресечната точка с оста: (·) А (2, 0) и (·) В (1, 0).
С «Oy» ос: (·) C (0, 2).

Как да се определи на каква стойност на х функция може да отнеме положителни или отрицателни стойности

Припомняме ви, че когато работата се казва "отнема ценности" - това е "Y" ценности. С други думи, трябва да се отговори на въпроса: за какво стойности на «х», координират «у» е положителна или отрицателна.

За да се определи функцията на графиката, когато функцията се положителни или отрицателни стойности трябва да бъдат:

• срещнат директно през точките на места, където графиката пресича «Вол» ос;
• определи функция положителна или отрицателна стойност поема интервалите между линиите проведени;
• напишете отговора за всеки период на относителна «х».

Използване на графиката на квадратна функция е показано на фигура отговор: При което стойностите на «х» функция отнема 1) положителни стойности; 2) отрицателни стойности.

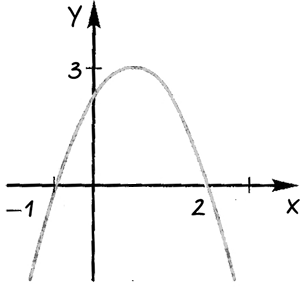
Чрез точките, в които графиката на функцията пресича «Вола» директна ос.

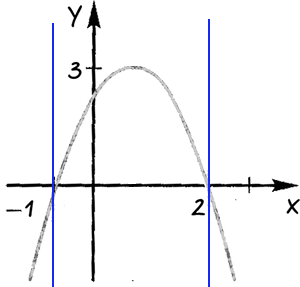
Ние дефинираме региона, където функцията отнема отрицателни или положителни стойности.

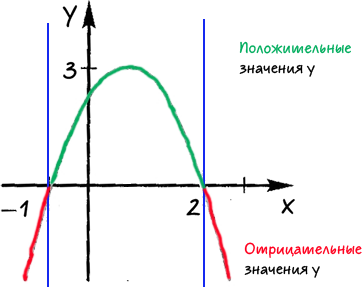
Влезте през всеки от полученото в зоната, която заема стойности «х» във всяка от избраните области.

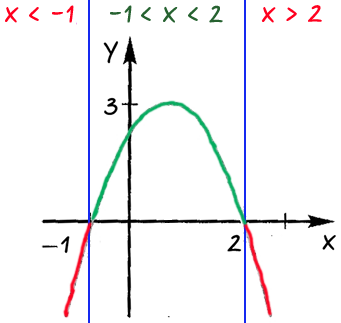
Отговор: в «х 2" функция може да отнеме отрицателна стойност; когато "-1