Как да се опрости корен квадратен

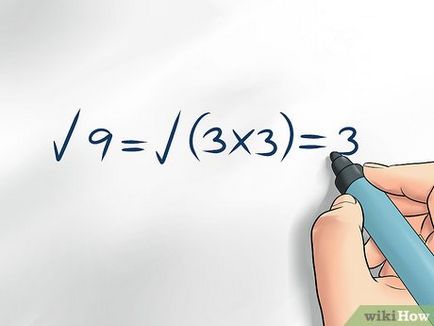
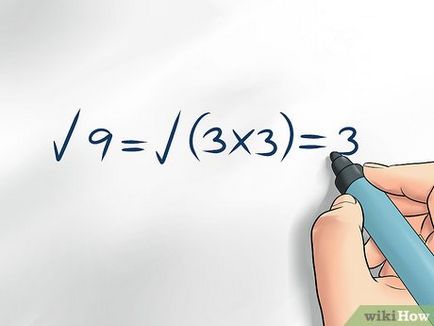
Стремежът към опростяване на квадратния корен - е да го пренапише във форма, която е по-лесно да се използва при изчисляването. Разширяване на броя на факторите - е да се намерят две или повече числа, които, когато се умножат, дават първоначалния брой, като 3 х 3 = 9. Намиране на множители, можете да опростят корен квадратен или дори да се отърве от него. Например, √9 = √ (3x3) = 3.

Ако корен квадратен е четно число, го разделете на корен квадратен 2. Ако броят им е странно, опитайте се да го разделете на 3 (ако числото не се дели на 3, го разделете на 5, 7 и така нататък през списъка с прости числа). Сподели radicand изключително на простите числа, тъй като всяко число може да се разлага на основните фактори. Например, не е нужно да се разделят на броя на корен квадратен от 4, защото 4 се дели на две, а вече сте споделили radicand е 2.

• 2
• 3
• 5
• 7
• 11
• 13
• 17

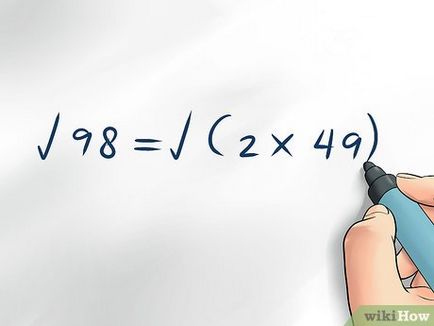
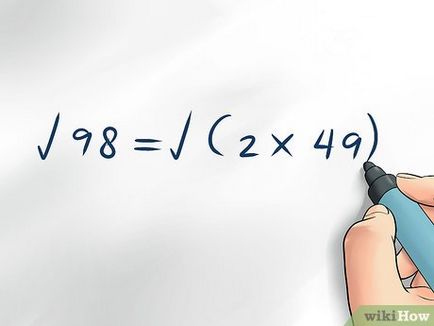
Препишете задача като корен квадратен от произведението на две числа. Например, опрости √98: 98 ÷ 2 = 49, така че 98 х 2 = 49. Rewrite задача като: √98 = √ (2 х 49).

Продължи разширяване на брой, докато по корена ще остане продукта от две идентични номера и други номера. Това има смисъл, когато се мисли за смисъла на корен квадратен: √ (2 х 2) е числото, което, когато се умножи по себе си, ще бъде равен на 2 х 2. Очевидно е, че номер 2! Повторете горните стъпки за нашия пример: √ (2 х 49).

• 2 вече е максимално опростена, тъй като тя е просто число (вж. Списъкът на прости числа по-горе). Затова фактор броя 49.
• 49 за 2, 3, 5, не е разделена. Ето защо, да преминете към следващия брой премиер - 7.
• 49 ÷ 7 = 7, така че 49 = 7 х 7.
• Препишете задача като: √ (2 х 49) = √ (2 х 7 х 7).

Опростяване на корен квадратен. Тъй като при корена е продукт на 2 и два еднакви номера (7), можете да направите няколко знака на корена. В нашия пример: √ (2 х 7 х 7) = √ (2) √ (7 х 7) = √ (2) х 7 = 7√ (2).

• След като в основата на имаш две от един и същи номер, можете да спрете разлагането на номера на фактори (ако все още може да се разшири). Например, √ (16) = √ (4 х 4) = 4. Ако продължите номера разпадане факторинга, можете да получите един и същ отговор, но са направили много изчисления: √ (16) = √ (4 х 4) = √ (2 х 2 х 2 х 2) = √ (2 х 2) √ (2 х 2) = 2 х 2 = 4.

Някои корени могат да опростят многократно. В този случай, номерата трябва да бъдат извадени от под знака корен и броя изправена корен умножават. Например:

• √180 = √ (2 х 90)
• √180 = √ (2 х 2 х 45)
• √180 = 2√45, но 45 може да се отчете и отново се опрости корен.
• √180 = 2√ (3 х 15)
• √180 = 2√ (3 х 3 х 5)
• √180 = (2) (3√5)
• √180 = 6√5

Ако не можете да получите две от един и същи номер в рамките на радикала, а след това корен не може да бъде опростен. Ако се разпространява радикален израз на произведението на основните фактори, както и между тях не съществуват две еднакви числа, а след това този корен не може да бъде опростен. Например, опитайте се да се опрости √70:

• 70 = 35 х 2, така √70 = √ (2 х 35)
• = 7 х 35 5, така √ (35 х 2) = √ (7 х 5 х 2)
• Всички три фактора са прости, така че те вече не могат да бъдат отчетени. Всички три фактора са различни, така че няма да бъде в състояние да направи едно цяло от под знака корен. Следователно √70 не може да бъде опростен.

Не забравяйте, няколко квадратчета с прости числа. Квадратът на броя на завъртанията в изграждането на втора степен, т. Е. умножено по себе си. Например, 25 - точен квадрат, защото 5 х 5 (5 2) = 25. След като спомни поне една дузина на квадрати, можете бързо да се опрости корените. Ето и първите десет пълни площади:

• 01 февруари = 1
• 2 2 = 4
• 02 Март = 9
• 02 април = 16
• Май 2 = 25
• 02 юни = 36
• 2 юли = 49
• 08 февруари = 64
• 02 сеп = 81
• Февруари 10 = 100

Ако под знака на квадратния корен на площада можете да видите пълния, а след това да се отървете от знака за корен (√) и напишете корен квадратен от точен квадрат. Например, ако в рамките на корен квадратен знак е номер 25, който е корен 5, тъй като 25 е точен квадрат.

• √1 = 1
• √4 = 2
• √9 = 3
• √16 = 4
• √25 = 5
• √36 = 6
• √49 = 7
• √64 = 8
• √81 = 9
• √100 = 10

Подредете броя подкоренен на продукта на точен квадрат и друг номер. Ако забележите, че радикалната израз може да бъде разложен на продукта на точен квадрат и някои цифри, след това ще спести време и усилия. Ето няколко примера:

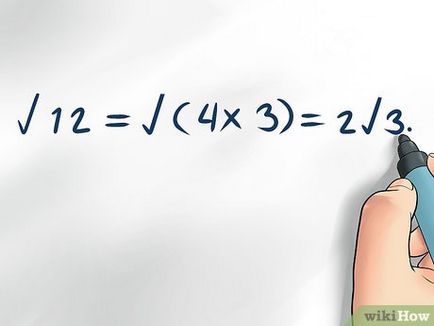
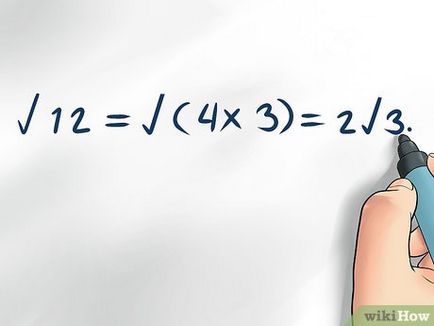
• √50 = √ (25 х 2) = 5√2. Ако броят завършва с корен квадратен от 25, 50 или 75, винаги можете да го разшири в работата на 25 и някои номер.
• √1700 = √ (100 х 17) = 10√17. Ако radicand завършва на 00, винаги можете да го разшири дейността си в един продукт 100, а някои номер.
• √72 = √ (9 х 8) = 3√8. Ако сумата от цифрите е равен на корен квадратен от 9, винаги можете да го разшири дейността си в продукт на 9 и някои цифри.
• √12 = √ (4 х 3) = 2√3. Винаги проверявайте дали radicand разделен на четири.

Поставете radicand да работят по-добра площади. В този случай, се възползват от тях под знака корен и се размножават. Например:

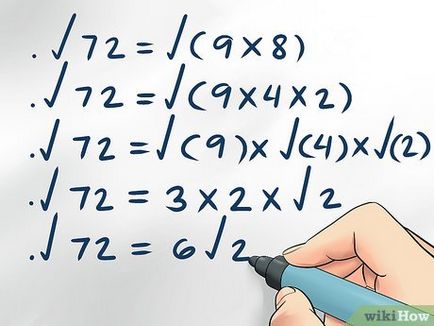
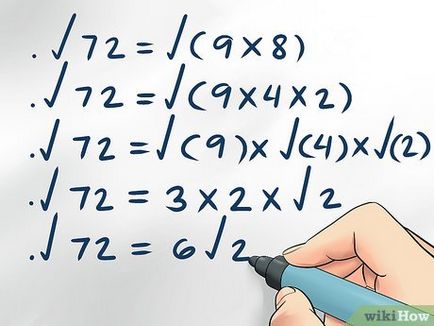
• √72 = √ (9 х 8)
• √72 = √ (9 х 4 х 2)
• √72 = √ (9) х √ (4) х √ (2)
• √72 = 3 х 2 х √2
• √72 = 6√2