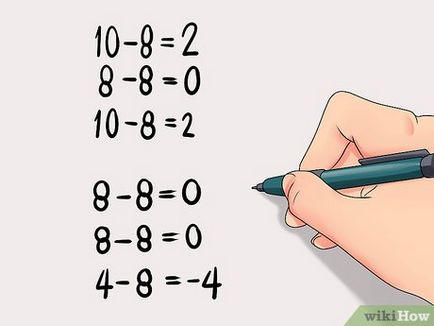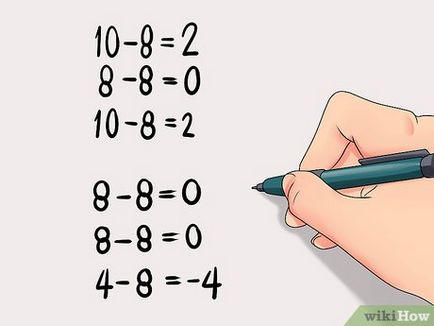стъпки Редактиране
Част 1 от 3: Средна Редактиране
Вземете набор от данни. Средна стойност - е важна величина за статистически изчисления. [3]
- Определяне на размера на номера в набора от данни.
- Числата в комплекта са много различни една от друга или са в непосредствена близост (на различни частични части)?
- Какви са числата в масива от данни? Тестови резултати, четене на пулса, височина, тегло и така нататък.
- Например, един набор от тестове брой: 10, 8, 10, 8, 8, 4.
За да се изчисли средните стойности трябва всички от този набор от данни. [4]
- Средна стойност - е средната стойност на всички числа в масива от данни.
- За да се изчисли средните стойности възлизат всичките си набор от данни и се делят на резултата от общия брой на числа в комплекта (н).
- В нашия пример, (10, 8, 10, 8, 8, 4) п = 6.
Съберете цялата си набор от данни. [5]
- В примера, даден броят 10, 8, 10, 8, 4 и 8.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Това е сумата на всички числа в набора от данни.
- Добави цифрите отново, за да се провери отговора.
Разделете сумата от числата от броя на номера (N) в пробата. Тук ще намерите средната. [6]
- В нашия пример, (10, 8, 10, 8, 8, 4) п = 6.
- В този пример, сумата от номера равна на 48. По този начин, се разделят 48 за п.
- 48/6 = 8
- Средната стойност на тази проба е осем.
Част 2 от 3: Дисперсия Редактиране
Изчислява дисперсията. Тази мярка разсейване около средната стойност. [7]
- Тази стойност ви дава представа за това как разсеяна данни за вземане на проби.
- с малка дисперсия на пробата включва данни, които не се различава много от средната стойност.
- висока дисперсия проба включва данни, които се различават от средната стойност.
- Дисперсията често се използва за сравняване на разпределението на двата набора от данни.
Изваждане на средната стойност на всеки номер в масива от данни. Ще научите как всяка стойност в масива от данни е различна от средната за страната. [8]
- В нашия пример, (10, 8, 10, 8, 8, 4), средната стойност е равна на 8.
- 10-2 = 8; 8-8 = 0, 10-2 = 8 8 - 0 = 8, 8-8 = 0 и 4-8 = -4.
- Смятате изваждане отново, за да се провери всеки отговор. Това е много важно, тъй като ще са необходими на получените стойности при изчисляването на други количества.
Squaring всяка стойност, който сте получили в предишната стъпка. [9]
- Чрез изваждане на средната стойност (8) от всяка проба (10, 8, 10, 8, 8 и 4) следните стойности имаш 2, 0, 2, 0, 0 и -4.
- Асансьор тези стойности в квадрат: 2 2. 0 2. 2 2. 0 2. 0 2. и (4) 2 = 4, 0, 4, 0, 0 и 16.
- Проверете отговорите преди да се пристъпи към следващата стъпка.
Сгънете квадратите на стойности, тоест, намери сумата от квадратите. [10]
- В нашия пример, стойностите на квадратите: 4, 0, 4, 0, 0 и 16.
- Припомнете си, че стойността, получена чрез изваждане на средната стойност от всеки от пробата: (10-8) ^ 2 + (8-8) ^ 2 + (10-2) ^ 2 + (8-8) ^ 2 + (8-8 ) ^ 2 + (4-8) ^ 2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумата от квадратчета е 24.
Разделете сумата от квадратите на (п-1). Не забравяйте, че п - е броят на данни (номера), вашата проба. По този начин, можете да получите на промяната. [11]
- В нашия пример, (10, 8, 10, 8, 8, 4) п = 6.
- N-1 = 5.
- В нашия пример, сборът от квадратите е равен на 24.
- 24/5 = 4.8
- Дисперсията на пробата е 4.8.
Вземи дисперсията за изчисляване на стандартното отклонение. [12]
- Не забравяйте, че дисперсията - мярка разсейване около средната стойност.
- Стандартно отклонение - е подобна на стойността, която описва естеството на разпределението на данните в пробата.
- В нашия пример, дисперсията е 4.8.
Вземете корен квадратен от дисперсията да намерите на стандартното отклонение. [13]
- Обикновено, 68% от данни са в рамките на едно стандартно отклонение от средната стойност.
- В нашия пример, дисперсията е 4.8.
- √4,8 = 2.19. Стандартното отклонение на извадката е равен на 2.19.
- 5 от 6 числа (83%) от пробата (10, 8, 10, 8, 8, 4) е в рамките на едно стандартно отклонение (2.19) от средната стойност (8).
Уверете се, изчисляване на средната стойност, дисперсията и стандартното отклонение. Това ще ви позволи да се провери своя отговор. [14]
- Задължително изчисление запис.
- Ако в процеса на проверка на изчисленията, ще получите различна стойност, проверете всички изчисления от самото начало.
- Ако не можете да намерите къде да се направи грешка, направи изчисление от самото начало.