Как да намерите основата на трапеца
За да зададете като четириъгълник, трапец като трябва да се определят най-малко три страни. Ето защо, например, е възможно да се помисли за проблема, в състоянието, в който се посочва дължината на диагоналите на трапец. и един от страничните вектори.

Фигура условия на проблема е показано на фигура 1. В този случай трябва да се приеме, че по-горе трапец - четириъгълник AVCD, където предварително определената дължина на диагоналите AC и BD, и странична страна AB, представено с вектор (брадва, AY). Данните за получените изходни ни позволяват да намерим две osnovaniyatrapetsii (и двете отгоре и отдолу). В конкретен пример по-ниската база на АД ще се намери на първо място.
Помислете триъгълника ABD. Дължината на едната си страна AB е равна на силата на. Нека | а | = SQRT ((брадва) ^ 2 + (ай) ^ 2) = а, а след това cosf = брадва / SQRT (((брадва) ^ 2 + (ай) ^ 2), тъй като посоката косинус на нека е посочено. р има диагонал дължина на BD и АД желаната дължина и. След това, от косинус, р ^ 2 = а ^ 2 + х ^ 2-2axcosf. или 2-2axcosf х ^ + (а ^ 2-р ^ 2) = 0 ,
Разтвори на квадратното уравнение: Х1 = (2acosf + SQRT (4 (а ^ 2) ((cosf) ^ 2) -4 (а ^ 2-р ^ 2))) / 2 = acosf + SQRT ((а ^ 2) ((cosf) ^ 2) - (а ^ 2-р ^ 2)) == на * брадва | SQRT (((ах) ^ 2 + (AY) ^ 2) + SQRT ((((а) ^ 2) (брадва ^ 2)) / (брадва ^ 2 + ай ^ 2)) - а ^ 2 + р ^ 2) = АД.
За горната основа слънце (дължината в намирането на решения също определени х) се използва модул | а | = а, и втори диагонал BD = р и косинус на ъгъла ABC, което е ясно, равна на (р-р).
Следваща се счита за триъгълник ABC, които, както и преди, е приложил косинус теорема, и там е следващото решение. Като се има предвид, че COS (п, п) = - cosf, въз основа на решение на AD, можем да напиши следната формула чрез заместване р с Q: BC = - с * брадва | SQRT (((ах) ^ 2 + (AY) ^ 2 ) + SQRT ((((а) ^ 2) (брадва ^ 2)) / (брадва ^ 2 + ай ^ 2)) - а ^ 2 + р ^ 2).
Това уравнение е квадратна и съответно има две корени. По този начин, в този случай е да се подберат само корените, които имат положителна стойност, тъй като дължината не може да бъде отрицателен.
PrimerPust трапец ABCD в странична стена AB се дава с вектора на (1, sqrt3), р = 4, Q = 6. Намери osnovaniyatrapetsii .Reshenie. Използването на алгоритми, получени по-горе могат да бъдат написани: | а | = а = 2, cosf = 1/2. AD = 1/2 + SQRT (4/4 -4 + 16) = 1/2 + SQRT (13) = (SQRT (13) 1) /2.BC=-1/2+sqrt (-3 + 36 ) = (SQRT (33) -1) / 2.
Trapeze счита четириъгълник, в който двете страни са успоредни, а другите две не. Височината на трапеца, се нарича сегмент начертава перпендикулярно между две успоредни линии. В зависимост от суровите данни, че може да се изчисли по различни начини.
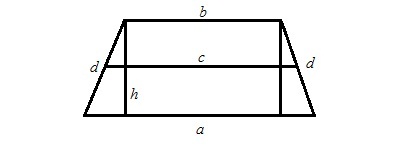
- Познания Гарнитура бази разреза трапец, както и, евентуално, неговата област и / или периметъра.
Един от начините да се изчислява площта на трапеца е продукт на височината и средната линия. Да приемем, че е налице равнобедрен трапец. След това височината на равнобедрен трапец с основи А и Б, на площ S и периметър P се изчислява, както следва:
Н = 2 х S / (Р-2 х г). (Вж. Фигура 1)
Ако само известна площ на трапеца и основа, формулата за изчисление височина може да бъде получен от областта на трапец формула S с = 1 / 2Н х (А + В):
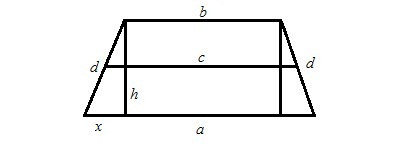
Да приемем, че е трапец с едни и същи данни, както е на фигура 1. височина 2 Draw, ние се получи правоъгълник, чиито страни са две по-малки краката на правоъгълни триъгълници. Означаваме малки ролки за х. Установено е чрез разделяне на разликата между дължините на по-големи и по-малки бази. След това, от теоремата на Питагор квадратен от височината, равен на сбора от квадратите на хипотенуза и крака г х. Извличане на основата на тази сума и да получите височина ч. (Фиг. 2)
А математическа фигура с четири ъгли, се нарича трапец, ако двойката е на неговите противоположни страни паралелно и друга двойка - не. Паралелни страни призоваха osnovaniyamitrapetsii. другите две - страна. В правоъгълен трапец един от ъглите на страната на - линия.
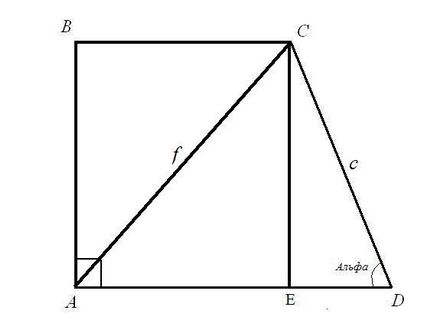
Задача 1.Locate база BC и AD правоъгълен трапец. ако знаем дължината на диагонала AC = F; странична дължина CD = С и ъгъл на своя ADC = α.Reshenie: Да разгледаме правоъгълен триъгълник CED. Известен хипотенуза с и ъгълът между хипотенузата и ЕРП на крака. Вземете страни дължина CE и ED: ъгъл от формула CE = CD * грях (ADC); ED = CD * COS (ADC). Така че: CE = C * sinα; ED = C * cosα.
Помислете за един правоъгълен триъгълник ACE. Хипотенуза AC и CE крак ли, че, да отстрани AE от върховенството на правоъгълен триъгълник: сборът от квадратите на краката е равен на квадрата на хипотенузата. Така че: AE (2) = AC (2) - CE (2) = F (2) - в * sinα. Изчислява се корен квадратен от дясната ръка. Намерили сте горната основа на правоъгълен трапец.
AD база дължина е сумата от дължините на двете отсечки AE и ED. AE = корен квадратен (е (2) - в * sinα); ED = C * cosα) .Itak: AD = корен квадратен (е (2) - в * sinα) + C * cosα.Vy намерено правоъгълна долната основа на трапец.
Задача 2.Locate база BC и AD правоъгълен трапец. ако знаем дължината на диагонала BD = F; странична дължина CD = С и ъгъл на своя ADC = α.Reshenie: Да разгледаме правоъгълен триъгълник CED. Да се намери дължината на маркировката на страни и ED: CE = CD * грях (ADC) = C * sinα; ED = CD * COS (ADC) = C * cosα.
Помислете правоъгълник ABCe. Чрез собственост на правоъгълник AB = CE = C * sinα.Rassmotrite правоъгълен триъгълник ABD. Чрез собственост на правоъгълен триъгълник квадрата на хипотенузата е равен на сбора от квадратите на другите две страни. Следователно, АД (2) = BD (2) - AB (2) = F (2) - в * sinα.Vy намерено долната основа на трапец правоъгълна АД = корен квадратен (е (2) - в * sinα).
По правило правоъгълник BC = AE = АД - ED = корен квадратен (е (2) - в * sinα) - * cosα.Vy установено с горната основа на правоъгълен трапец.
Малък основа на трапеца е успоредна на една от неговите страни имат минимална дължина. Изчислете тази стойност по няколко начина, с помощта на някои данни.
Ако знаете, че дължината на две - голяма база от трапеца и средната линия - използвана за изчисляване на най-малката основа на трапец имота. Според нея средната линия е идентичен с половината от основния трапец. В този случай, най-малката основа е равен на разликата от два пъти дължината на средната линия и дължината на голяма база на фигурата.
Ако такива параметри са известни трапец като площ, височина, дължина на голямата основа, изчисляването на най-малкия основата на фигурата, за да доведе на база площта на формулата на трапец. В този случай, крайният резултат, получен чрез изваждане от разликата на два пъти личната зона и височината на такъв параметър като дължината на голяма трапецовидна основа.
Дължината на малката страна на правоъгълен трапец се изчислява по друг начин. Този параметър е равна на произведението от дължината на втората страна и синуса на остър ъгъл към него полегнало положение. В тези случаи, когато ъгълът е известно, най-малката страна на приравнена към височината на трапеца и се изчислява с помощта на Питагоровата теорема. Най-малката страна на правоъгълен трапец открие с помощта на косинус теоремата: s² = ² + b²-2ab * cosα; където А, В, С представляват страните на триъгълника; α е ъгълът между страни а и Ь.