Как да намерите матрицата долепени
Кофактори - е един от понятията матрица алгебра прилагат към елементите на матрицата. Намирането кофактори е едно от действията на алгоритъма за определяне на обратна матрица и отдела за работа матрица.

Matrix алгебра е не само най-важните раздели на висшата математика, но и набор от методи за различни приложения, като изготви система от линейни уравнения. Matrix, използвани в икономическата теория и в изграждането на математически модели, като линейното програмиране.
Линейна алгебра описва и изследва много операции за матрици, включително сумиране, умножение и деление. Последният ефект е условно, той всъщност е умножаване с обратен матрицата на второто на. И след това отидете на помощта на кофактори на елементите на матрицата.
Понятието алгебрични допълнения директно следва от другите две основни дефиниции на теория матрица. Това е най-определящ фактор и непълнолетния. Детерминанта на квадратна матрица е номер, който се получава по следната формула въз основа на стойностите на елемента: Δ = a11 • А22 - А12 • A21.
Мала Matrix - е неговата детерминанта, редът на който е един по-малко. Мала всеки елемент, получен чрез отстраняване от номерата на матрица редове и колони на позицията на съответния елемент. Т.е. Мала М13 е еквивалентно на детерминантата на матрицата, получен след изтриване на първия ред и третата колона: M13 = A21 • А32 - А22 • A31.
Да се намери матрица алгебрични допълнения, е необходимо да се определи съответната непълнолетния от нейните елементи с определен знак. Знакът зависи от това какво положение трябва елемента. Ако размерът на хоризонталните и вертикални номера - четно число, а след това кофактор е положително число, ако е нечетен - отрицателна. Т.е.: Aij = (-1) ^ (I + J) • MIJ.
Primer.Vychislite кофактори.
Матрицата нарича маса, състояща се от определените стойности, и с размери в п колони и редове м. Системата от линейни алгебрични уравнения (SLAE) висок ред може да бъде решен чрез свързания с него матрица - система матрица и разширената матрица. Първият е масив система коефициенти на неизвестните променливи. При добавяне на този масив колона матрица В се получава свободни членове SLAE разширени матрица (А | Б). Изграждане на разширената матрица е една от стъпките в решаването на произволни уравнения.

Като цяло, системата от линейни уравнения може да бъде решен чрез заместване, но за линейни системи за едрогабаритни това изчисление е много време. И в този случай, често използвате свързани матрица, включително и разширения.
Запишете дадена система от линейни уравнения. Прекарайте своята реализация чрез организиране на факторите в уравненията, така че същите неизвестни променливи в системата подредени строго една над друга. Безплатни курсове без неизвестен трансфер към друга част от уравнението. Когато пренареждане на условията и обмисли прехвърлянето им знак.
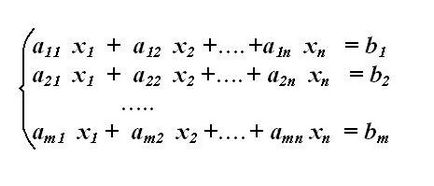
Определяне на матрицата на системата. За този отделен списък коефициентите на неизвестните променливи Слау. Необходимо е да се напише в същия ред, както те се появяват в системата, т.е. първото уравнение на първия коефициент определен в първия ред и първата колона на матрицата. Редът на редовете на матрицата съответства на новия ред на системата от уравнения. Ако една от неизвестните в системата на уравнение не е на линия, а след това му коефициент е равен на нула - нула запълване в матрица от позицията на реда. Получената система матрица трябва да бъде квадрат (т = п).
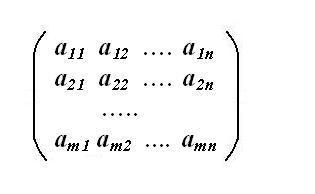
Намерете най-разширената матрица на системата. Безплатни фактори в уравненията на познатата система на равенство записват в отделна колона, запазвайки същия ред от редовете. В квадратна матрица на правото на вертикалната линия сложи всички коефициенти. По-долу добави получената колона на свободни условия. Това ще бъде увеличен матрица първоначален размер SLAE (m, п + 1), където m - брой на редовете, п - брой колони.
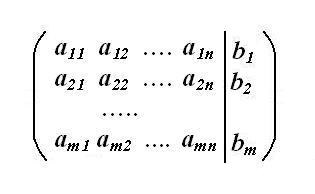
Това е за разширената матрица по метода на Гаус изчислява корените на система за линейни алгебрични уравнения. Гаус е един от най-активно използваните методи за решаване на линейната висок ред.
- Разширена система матрица