Изчисляване на производни
Девиз: Един попита: "Какво е най-деривативни се различава от продукта?" "Дериватите се изучават в клас по математика, и на продукта - урок литература" - последвано от реакция на студент.
В епиграф описана реалната ситуация на моята практика. Въпросът възниква, когато зеницата заплете правила диференциация функции, по-специално, той не е в състояние да се определи производно произведение на две функции. За да се избегне такова тълкуване на тази статия, за да ви напомня, че ние правим само математика, и тук, терминът "продукт" означава резултата от умножението, а "производно" е границата на отношението на функцията за увеличение на нарастване на аргумента, когато последният клони към нула. Процесът на изчисление се нарича диференциация производно.
Производни на елементарни функции, по дефиниция, т.е. през границата се изчислява само веднъж на лекция (в класната стая), за да се осигури връзка и лимит производно. В бъдеще, ние се интересуваме само при практическото прилагане на тази концепция, така че да се изчисли дериватив, са готови формули и правила за диференциране на функции.
Тук ще разгледаме как да и как не трябва да се изчисли на производните, но, за съжаление, много студенти и дори ученици правят.
Как да се изчисли производни
Писано е навсякъде, във всички учебници и на различни места в мрежата.За производни, е необходимо, с помощта на един или друг източник, все още се научат формула диференциация на елементарни функции. Например, виж подробно статия на масата на производни и примитиви. За по-сложни от табличен, обединените функциите на правилата за изчисляване на производно на сумата, продуктът, фракцията. Съответните математическите изрази като можете да намерите навсякъде. Но, по мое мнение, правилата на диференциация на функциите по-добро определяне и запомнят думите:
- Постоянен коефициент може да се приема като знак на деривата.
- Производно на сума, равна на сумата от производни.
- Производното продукт е равно на "производно на първия фактор, умножена по втората производна плюс Вторият фактор, умножена по първата".
- Производното на фракция е равна на "производно на числителя умножена по знаменател, минус производно с знаменател, умножена по числителя разделен на знаменател в квадрат."
- Производното на съставния функция е производно на външната функция, умножена по производно на вътрешната и изчисленото "продължаване" на масата.
Как да не се изчисли производни
- На първо място, не е необходимо да се усложни проста.
- Не бъркайте условията и факторите (сума и за продукти).
- Не бъркайте мощност-Ха и експоненциална функция брадвата.
- Не трябва да се забравя, че производното на съставна функция се оценява "продължаване" до таблична формула.
- Не се притеснявайте да се сложи скоби.
В повечето от следните примери илюстрират изпълнения изчислителни производни, в които
1. Изчисленията се извършват много слабо. с очевидни грешки;
2. правото, но не е оптимално. т.е. дълго и с вероятна грешка в невнимание;
3. доста добре.
Забележка за правилото, че сложих номер едно.
Ако работата е един от факторите, е постоянна, тогава не е необходимо да се използва правилото на производни произведения. Освен това, не е необходимо да се направи това, защото тя често е придружен от такава грешка операция. Постоянен коефициент може да се приема като знак на деривата!
Ако фракция числителя или знаменателя е константа, тогава не е необходимо да се използва правилото за деривати фракции. Това действие на учениците и студентите по-често се придружава от грешки. Постоянен коефициент може да се приема като знак на деривата!
Най-често срещаната грешка в тези примери - да забрави да се сложи на бара (наименованието на деривата) на броя, или да го постави, и "не виждам" следващото действие, т.е. не се вземат под внимание, че производна константа (брой) е равна на нула.
Тук, за първия и третия примери за простотата и качеството на подхода на скоби в налагането на числен коефициент, е очевидно. Но това не е толкова ясно за втория пример, където знаменателя е тригонометрични функции. Освен това, съгласен съм, че за тези студенти, които имат лошо производно сложна функция (правило 5), по-предпочитано в този пример може да бъде правилото за диференциация фракция.
Въпреки това, в продължение на няколко други функции, особено за власт, просто трябва знаменател "завой" в числителя, и корени - отчасти защото в този случай можем да използваме най-простите и най-запомнящите се таблична формула (х # 945; ) = # 945 х # 945; - 1.
В тези два примера, представен обичайните грешки в диференциацията на фракцията с постоянна, и в примера по-долу, е необходима за прехода от корена на фракционна силата защото в противен случай често се забравя, че такава функция не е таблица, и трябва да се диференцира според правилото за композитни функции.
Постоянно план диференциация с нулира-постоянен фактор за диференциация се поддържа.
Освен това, по някаква причина, много ученици деривати на функция у = х 2 + 0.1 по-лесно да се изчисли от същия тип производно (0.1 + х 2). И за производно на функция у = 0.1 х 2 често реализира наличието на първото правило, а за (х 2 х 0.1) "не.
Когато направите този вид грешка, не забравяйте, че Първообразът на сума, която не се променя, а Първообразът на факторите не се променя продукта. Пренареждане тях, както предпочитате, и внимателно се прилага първия или втория правилата за получаване на производни.
В първия случай, променливата е в основата на степента, четем: "X за силата на". Във втория - на променливата в експонентата, четем: "и силата на X". Характеристики на различни формули за изчисляване на производни различни. Cm. Таблица.
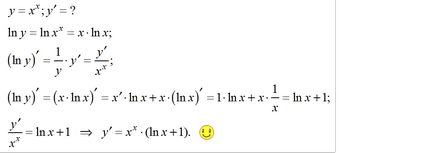
Това е сложна функция, която не е пряко свързана с всеки клас на мощност, нито демонстрация клас. За да изчислим производната в такива случаи често се налага да се получи предварителна конверсия. Например, първият експресията е логаритъм, след като производните на двете страни на нейните променливи и накрая постигнато уравнение за намиране на желаното производно на променливата х.
Комплекс функция, тази функция не е в пряка зависимост от променливата, а от друга функция. С други думи, неговата стойност не може да бъде изчислена в една стъпка. Например, функция Y = sinx2 и Y = грях 2 х са сложни. Нека да видим как са изчислени стойностите им, например, когато х = 2.
За функция у = sinx2 първо трябва да се постави в квадрат х 2 2 = 4, и след това да се изчисли стойността на задължително 4-DX. Ние правим това с помощта на калкулатора: sin4 = -0,75680249530792825. ≈ -0,76 (не забравяйте, че се смятат за тригонометричните функции на аргументи, както са дадени в радиани).
За функция у = грях 2 х първо определят синуса на 2-помощта на калкулатора: sin2 = 0,9092974268256816. и след това се издигне стойността на квадрат грях 2 2 = (.9092974268256816.) 2 = .82682181043180595. ≈ 0,83.
По този начин, за първи път се изчисли стойността на вътрешния функция и след това да го използвате като аргумент навън.
Според петото върховенството на диференциация, при определяне на производно необходимостта да се правят точно обратното - първо да се изчисли на производната на външната функция на тезата си, а след това го умножете по производната на вътрешната страна.
Както споменах, най-често грешки в тази операция. Грешки могат да бъдат много различни, следните три общ.
Първа грешка) Не можете да приложите само правото правилото "не се отбележи, че" сложна функция.
В следната формула, и силата на диференциация на тригонометрични функции, използвани не последователно но едновременно, производно неправилно изчислява в един етап.
2-ра грешка) Не мога да разбера, когато вътрешните и външните функции къде.
В следващия пример експонентата е над х. т.е. горе аргумент следователно степента на функцията на вътрешната и външната синус. Ученик отне така или иначе, реших, че синуса на квадрат и е направил грешка.
За да се отървете от този вид грешка, научете се да анализираме сложна функция за разделяне на вътрешната от външната страна, просто трябва да гледате реда, в който сте извършва изчисления, и диференциация в обратен ред. Възможно е да се осигури липсващите скобите, а ако все още имате трудности, да се въведе допълнителен нотация. Що се отнася до степента, можете да си спомните това - за това как определянето стои експонат, който е основата му (е повдигнато).
Пример 12.
Там се използва в края на тригонометрични синуса на формулата за двойно ъгъл, за да се запишете отговора в най-компактна форма.
Пример 13.
Тук в края на факторите и пренаредени, за да напишете отговор в по-компактен и електронен формат.
Трета грешка) Правилото не се използва до края на
След като се взема под внимание, че функцията е сложен и ще са достатъчни. И ако функцията е вградена по няколко пъти? Например, корен квадратен от сумата на логаритмите на две различни основи, от които зависи от sinx. а втората на cosx. Или допирателната дъга, в зависимост от натуралния логаритъм, тоест, от своя страна, зависи от х на квадрат.
Пример 14.
Пример 15.
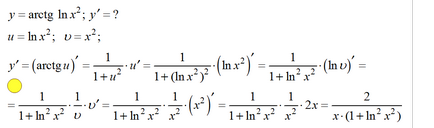
Предишният пример показва начина, по който чрез въвеждане на допълнителни символи. Но, по мое мнение, тя все още не е най-добрият начин за дълги изчисления. Най-добрият подход за разграничаване на съставна функция - скоби, които могат да се опрат на ясно или поне да засилят умението да си представите мислено.
Ние организираме скобите и постепенно разкриват им отвън навътре. Съдържанието на следващите скоби е променлива, през който получаването на формула фу "· (ф)". Производно фу "намери производни на масата, на мястото на формула X да ф. Ако всичко е направено правилно, процесът се допълва от факта, че съдържанието на последния, най-вътрешните скоби напълно съвпадат с един от масата на формули за производни.
