Докажете, че хипотенузата вече крак

Хипотенузата на правоъгълен триъгълник е винаги по-голям от който и да е от другите две страни. Защо? В действителност, дойде до такова заключение може да бъде няколко начина.

На първо място, ако знаете, че от друга страна по-голям ъгъл винаги е едно голямо парти, а двама правоъгълен триъгълник непряк остър ъгъл, доказателството ще изглежда много просто. Прав ъгъл е 90 °, а до него се намира хипотенуза. Острите ъгли на по-малко от 90 °, следователно страна разположена срещуположно на тях (краката) е по-малко от прав ъгъл, разположена срещуположно на хипотенузата.

Доказателството може да бъде изградена по различен начин. При един правоъгълен триъгълник ABC с прав ъгъл А. В този случай, а другите две са сегментите AB и AC, и дължината на хипотенузата BC.

то Рисуване върху отсечката BC BD равна на крака AB.

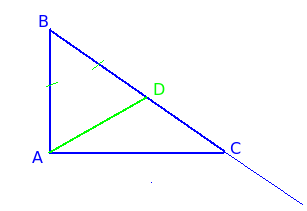
Ако преди новата ера върху AB, на точка D е от хипотенузата на BC, а след това крак върху хипотенузата. Ако AB е по-малко от преди новата ера, а след това на точка D ще лежи в интервала от преди новата ера, което означава по-малко от крака на хипотенуза.

Помислете триъгълника ABD. Тя равнобедрен, тъй като AB = BD от строителството. Както е известно в равнобедрен триъгълници базовите ъгли са винаги остри. Така ∠BAD <∠BAC, так как ∠BAC прямой. Следовательно, луч AD лежит внутри угла ∠BAC и пересекает гипотенузу BC, то есть лежит на ней, а не за ее пределами. Поскольку доказано, что BD

По същия начин може да се докаже, че крака и хипотенузата AC е по-малко от преди новата ера, ако се изгради един сегмент CD, равна на AC.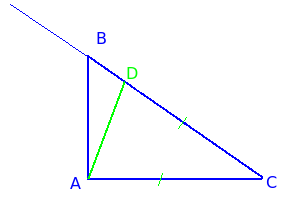

Тук ΔADC равнобедрен и ∠DAC <∠BAC. Следовательно луч AD лежит внутри ∠BAC и пересекает отрезок BC.